题目内容
 已知椭圆E1:
已知椭圆E1:| x2 |
| 10 |
| 2y2 |
| 5 |
| x2 |
| a2 |
| 2y2 |
| b2 |
| 3 |
| π |
| 6 |
(1)求椭圆E2的方程;
(2)求证:|AC|=|DB|;
(3)若|AC|=1,求直线l的方程.
分析:(1)根据当直线l过E2的上顶点时,直线l的倾斜角为
,且椭圆的离心率是
=
,建立方程,即可求得椭圆E2的方程;
(2)当直线l垂直x轴时,易求得|AC|=|DB|.当直线l不垂直x轴时,设l:y=k(x-
),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系得出x1+x2=x3+x4从而有|AC|=|DB|.
(3)由(2)知,|AC|=|CD|+2,先分类讨论:当直线l垂直x轴时,不合要求;当直线l不垂直x轴时,设l:y=k(x-
),由(2)知,x1+x2=x3+x4,x1x2,x3x4,利用弦长公式即可得关于k的方程,从而解决问题.
| π |
| 6 |
| c |
| a |
| ||
| 2 |
(2)当直线l垂直x轴时,易求得|AC|=|DB|.当直线l不垂直x轴时,设l:y=k(x-
| 3 |
(3)由(2)知,|AC|=|CD|+2,先分类讨论:当直线l垂直x轴时,不合要求;当直线l不垂直x轴时,设l:y=k(x-
| 3 |
解答:解:(1)∵b=1,
=
,∴a=2,b=1,
因此椭圆E2的方程为
x2+y2=1.
(2)当直线l垂直x轴时,易求得A(-
,-
),C(-
,-
),D(-
,
),B(-
,
)
因此|AC|=|DB|.
当直线l不垂直x轴时,设l:y=k(x-
)
由
得(1+4k2)x2+8
k2x+12k2-4=0 ①,
由
得(1+4k2)x2+8
k2x+12k2-10=0 ②,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则x3、x4是方程①的解,
x1、x2是方程②的解.∵x1+x2=x3+x4=
,
线段AB,CD的中点重合,∴|AC|=|DB|.
(3).由(2)知,|AC|=|CD|+2,
当直线l垂直x轴时,不合要求;
当直线l不垂直x轴时,设l:y=k(x-
),由(2)知,
x1+x2=x3+x4=
,x1x2=
,
x3x4=
,|CD|=
=
,
|AB|=
=
,
∴
+2=
,
化简可得:8k4-2k2-1=(4k2+1)(2k2-1)=0,
∴k=±
,
∴l:y=±
(x+
).
| c |
| a |
| ||
| 2 |
因此椭圆E2的方程为
| 1 |
| 4 |
(2)当直线l垂直x轴时,易求得A(-
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
因此|AC|=|DB|.
当直线l不垂直x轴时,设l:y=k(x-
| 3 |
由
|
得(1+4k2)x2+8
| 3 |
由
|
得(1+4k2)x2+8
| 3 |
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则x3、x4是方程①的解,
x1、x2是方程②的解.∵x1+x2=x3+x4=
-8
| ||
| 1+4k2 |
线段AB,CD的中点重合,∴|AC|=|DB|.
(3).由(2)知,|AC|=|CD|+2,
当直线l垂直x轴时,不合要求;
当直线l不垂直x轴时,设l:y=k(x-
| 3 |
x1+x2=x3+x4=
-8
| ||
| 1+4k2 |
| 12k2-10 |
| 1+4k2 |
x3x4=
| 12k2-4 |
| 1+4k2 |
| (1+k2)[(x1+x2)2-4x1x2] |
| 4k2+4 |
| 1+4k2 |
|AB|=
| (1+k2)[(x3+x4)2-4x3x4] |
| ||
| 1+4k2 |
∴
| 4k2+4 |
| 1+4k2 |
| ||
| 1+4k2 |
化简可得:8k4-2k2-1=(4k2+1)(2k2-1)=0,
∴k=±
| ||
| 2 |
∴l:y=±
| ||
| 2 |
| 3 |
点评:本题考查椭圆与椭圆的标准方程,考查直线与椭圆的位置关系,正确运用韦达定理是关键.

练习册系列答案
相关题目
 如图,已知椭圆E1方程为
如图,已知椭圆E1方程为 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
 ,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
,圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.  ,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值; 时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
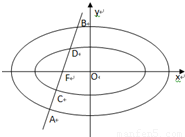
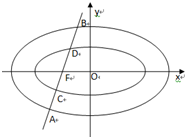
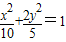 E2:
E2: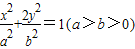 .E1与E2有相同的离心率,过点F(
.E1与E2有相同的离心率,过点F(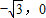 )的直线l与E1,E2依次交于A,C,D,B四点(如图).当直线l过E2的上顶点时,直线l的倾斜角为
)的直线l与E1,E2依次交于A,C,D,B四点(如图).当直线l过E2的上顶点时,直线l的倾斜角为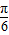 .
.