题目内容
18.下列命题中:①“?x0∈R,x02-x0+1≤0”的否定;
②“若x2+x-6≥0,则x>2”的否命题;
③命题“若x2-5x+6=0,则x=2”的逆否命题;
其中真命题的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①根据特称命题的否定是全称命题进行判断,
②根据否命题的定义进行判断,
③根据逆否命题的等价性进行判断.
解答 解:①“?x0∈R,x02-x0+1≤0”的否定是?x∈R,x2-x+1>0;∵判别式△=1-4=-3<0,∴?x∈R,x2-x+1>0恒成立,故①正确,
②“若x2+x-6≥0,则x>2”的否命题是“若x2+x-6<0,则x≤2”;由x2+x-6<0得-3<x<2,则x≤2成立,故②正确,
③命题“若x2-5x+6=0,则x=2”的逆否命题为假命题.
由x2-5x+6=0,则x=2或3,则原命题为假命题,则逆否命题也为假命题,故③错误,
故正确的命题是①②,
故选:C
点评 本题主要考查命题的真假判断,涉及含有量词的命题的否定,四种命题真假关系,比较基础.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
6.在等差数列46,43,40,37,…中第一个负数项是( )
| A. | 第15项 | B. | 第16项 | C. | 第17项 | D. | 第18项 |
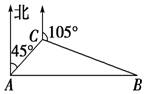 一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.
一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.