题目内容

12．已知函数$f（x）=\left\{{\begin{array}{l}{x+6，x≤2}\\{{3^x}-1，x＞2}\end{array}}\right.$，若f（a）=80，则f（a-4）=（　　）
A．0B．3C．6D．9

分析 先求出a的值，从而求出f（a-4）=f（0），代入函数的解析式即可．

解答 解：若a+6=80，解得：a=74，不合题意，
若3a-1=80，解得：a=4，
∴f（a-4）=f（0）=6，
故选：C．

点评 本题考查了求函数值问题，考查分段函数以及指数的计算，是一道基础题．

练习册系列答案
相关题目
16．i为虚数单位，则复数$\frac{1}{{3i}^{3}+{4i}^{4}+{5i}^{5}+{6I}^{6}}$的虚部为（　　）
A．$\frac{1}{4}$B．-$\frac{1}{4}$C．-$\frac{1}{4}$iD．$\frac{1}{4}$i
3．以椭圆$\frac{x^2}{4}+\frac{y^2}{2}$=1的焦距为实轴，短轴为虚轴的双曲线方程为（　　）
A．x2-4y2=2B．x2-y2=2C．x2-2y2=1D．2x2-y2=1
20．已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°，$\overrightarrow a=（2，0）$，$|{\overrightarrow b}$|=1，则$|{\overrightarrow a+2\overrightarrow b}$|=2$\sqrt{3}$．
7．A，B分别是y=kx和$y=-\frac{1}{k}x$与椭圆$\frac{x^2}{2}+{y^2}=1$的交点，点P在线段AB上，且$\overrightarrow{OA}•\overrightarrow{OP}=\overrightarrow{OB}•\overrightarrow{OP}$，当k变化时，点P一定在（　　）
A．双曲线x2-2y2=1上B．椭圆${x^2}+\frac{y^2}{2}=1$上
C．圆${x^2}+{y^2}=\frac{1}{3}$上D．圆${x^2}+{y^2}=\frac{2}{3}$上
17．已知过椭圆的右焦点且斜率为1的直线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）相交于A，B两点，若椭圆离心率为$\frac{1}{2}$，短轴长为2$\sqrt{3}$．
（1）求椭圆方程；
（2）求线段AB的长．
4．命题“空间两直线a，b互相平行”成立的充分条件是（　　）
A．直线a，b都平行于同一个平面B．直线a平行于直线b所在的平面
C．直线a，b都垂直于同一条直线D．直线a，b都垂直于同一个平面
1．设集合A={x|1＜x＜2}，B={x|x≤a}，若A⊆B，则a的取值范围是（　　）
A．a≥2B．a＞2C．a≥1D．a＞1
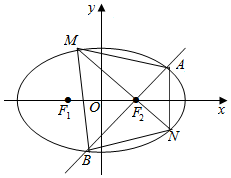2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1，F2，直线l经过F2且交椭圆C于A，B两点（如图），△ABF1的周长为4$\sqrt{2}$，原点O到直线l的最大距离为1．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过F2作弦AB的垂线交椭圆C于M，N两点，求四边形AMBN面积最小时直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网