Question

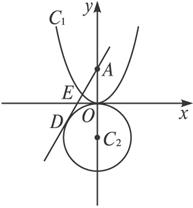
已知抛物线C₁∶y=x²+2x和C∶y=-x²+a，如果直线l同时是C₁和C₂的切线，称l是C₁和C₂的公切线，公切线上两个切点之间的线段为公切线段．

（1）a取什么值时，C₁和C₂有且仅有一条公切线？写出此公切线的方程；

（2）若C₁和C₂有两条公切线，证明相应的两条公切线段互相平分

 

Answer 1

答案：
解析：

（1）解：函数yx22x的导数y¢2x2，曲线C1在点的切线方程是：            ① 函数yx2a的导数y¢2x，曲线C2在点的切线方程是 即                         ② 如果直线l是过P和Q的公切线，则①式和②式都是l的方程，所以 消去x2得方程． 若判别式D44´21a0时，即时解得，此时点P和Q重合．即当时C1和C2有且仅有一条公切线，由①得公切线方程为． （2）证明：由（1）可知．当时C1和C2有两条公切线．设一条公切线上切点为：Px1，y1，Qx2，y2．其中P在C1上，Q在C2上，则有 x1x21，． 线段PQ的中点为．同理，另一条公切线段P¢Q¢的中点也是． 所以公切线段PQ和P¢Q¢互相平分．

提示：

本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力．