题目内容
16.数列{an}的通项公式an=n2•2n,求Sn.分析 利用错位相减法求即可求出前n项和.
解答 解:an=n2•2n,
∴Sn=1×2+4×22+9×23+…+n2•2n,
2Sn=1×22+4×23+9×24+…+(n-1)2•2n+n2•2n+1,
∴-Sn=1×2+3×22+5×23+7×24+…+(2n-1)•2n-n2•2n+1,
∴-2Sn=1×22+3×23+5×24+7×25+…+(2n-3)•2n+(2n-1)•2n+1-n2•2n+2,
∴Sn=2+2×22+2×23+2×24+2×25+…+2•2n-n2•2n+1-(2n-1)•2n+1+n2•2n+2,
∴Sn=2+22+23+24+25+26+…+2n+1-n2•2n+1-(2n-1)•2n+1+n2•2n+2-4,
=$\frac{2(1-{2}^{n+1})}{1-2}$-n2•2n+1-(2n-1)•2n+1+n2•2n+2-4,
=2n+2-n2•2n+1-(2n-1)•2n+1+n2•2n+2-6,
=2n+1( n2-2n+3)-6.
点评 本题考查了错位相减法求前n项和,关键是转化的思想,运算能力,属于中档题.

练习册系列答案
相关题目
9.将函数f(x)=sin(2x-$\frac{π}{2}$)的图象向右平移$\frac{π}{4}$个单位后得到函数g(x),则g(x)具有性质( )
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
7.“lnx<0”是“x<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知$\overrightarrow{a}$=2,$\overrightarrow{b}$=1,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=5,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
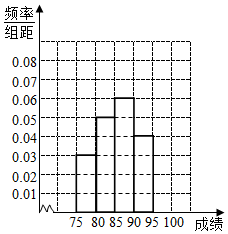 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.