题目内容
19．若实数a，b，c满足a+2b+3c=2，则当a2+2b2+3c2取最小值时，2a+4b+9c的值为5．分析 由条件利用柯西不等式求得当a2+2b2+3c2取最小值时，a、b、c的值，可得2a+4b+9c的值．
解答 解析：由柯西不等式得4=（a+2b+3c）2≤[a2+${（\sqrt{2}b）}^{2}$+${（\sqrt{3}c）}^{2}$][12+${（\sqrt{2}）}^{2}$+${（\sqrt{3}）}^{2}$]，
∴a2+2b2+3c2≥$\frac{4}{6}$=$\frac{2}{3}$，当且仅当$\frac{a}{1}$=$\frac{\sqrt{2}b}{\sqrt{2}}$=$\frac{\sqrt{3}c}{\sqrt{3}}$，即a=b=c=$\frac{1}{3}$时，取等号，
此时，2a+4b+9c=5，
故答案为：5．
点评 本题主要考查柯西不等式的应用，属于基础题．
练习册系列答案
相关题目
10．“φ=$\frac{π}{2}$”是“曲线y=sin（x+φ）关于y轴对称”的（ ）
| A． | 充要条件 | B． | 充分且不必要条件 | ||
| C． | 必要且不充分条件 | D． | 既不充分也不必要条件 |
7．过抛物线：y2=2px（p＞0）的焦点F作倾斜角为60°的直线l，若直线l与抛物线在第一象限的交点为A，并且点A也在双曲线：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线上，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{21}}{3}$ | B． | $\sqrt{13}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{5}$ |
11．设i是虚数单位，$\overline{z}$是复数z的共轭复数，若z$•\overline{z}$=2（$\overline{z}$+i），则z=（ ）
| A． | -1-i | B． | 1+i | C． | -1+i | D． | 1-i |
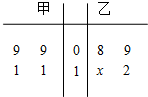如图所示，茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况．乙组某个数据的个位数模糊，记为x，已知甲、乙两组的平均成绩相同．