题目内容
设 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则
| A.3 | B.1 | C.-1 | D. |
D
解析试题分析:根据题意,由于设 为定义在
为定义在 上的奇函数,故有f(-x)=-f(x),当
上的奇函数,故有f(-x)=-f(x),当 时,
时, ,则可知
,则可知 由于f(0)=0,b=-1,故可知f(-1)=-3,故答案为D
由于f(0)=0,b=-1,故可知f(-1)=-3,故答案为D
考点:函数的奇偶性
点评:主要是考查了函数奇偶性的运用,属于基础题。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
若函数 为奇函数,则
为奇函数,则 =( )
=( )
A. | B. | C. | D.1 |
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有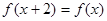 ,且当
,且当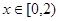 时,
时, ,则
,则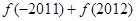 的值为
的值为
A.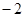 | B.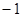 | C.1 | D.2 |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
定义在R上的函数f(x)在区间(-∞,2)上是增函数,且f(x+2)的图象关于x=0对称,则
| A.f(-1)<f(3) | B.f(0)>f(3) | C.f(-1)=f(3) | D.f(0)=f(3) |
如图,设a,b,c,d>0,且不等于1,y=ax , y=bx , y=cx ,y=dx在同一坐标系中的图象如图,则a,b,c,d的大小顺序( )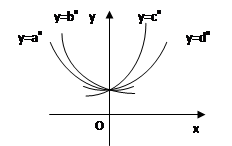
| A.a<b<c<d | B.a<b<d<c |
| C.b<a<d<c | D.b<a<c<d |
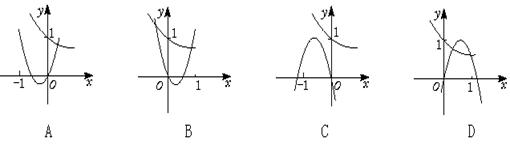
设 ,则此函数在区间
,则此函数在区间 内为 ( )
内为 ( )
| A.单调递增 | B.有增有减 | C.单调递减 | D.不确定 |
已知函数f(x)的定义域为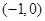 ,则函数
,则函数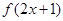 的定义域( )
的定义域( )
A.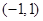 | B. | C.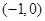 | D.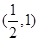 |
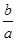 )x的图象只可能是( )
)x的图象只可能是( )