题目内容
如图,已知锐角∠AOB=2α内有动点P,PM⊥OA,PN⊥OB,且四边形PMON的面积等于常数c2,今以O为极点,∠AOB的角平分线OX为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线.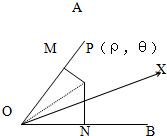
分析:设P的极点坐标为(ρ,θ),进而可分别)∠POM,∠NOM,OM,PM,ON,PN.根据四边形PMON的面积公式可得动点P的轨迹的极坐标方程化简后用x=ρcosθ,y=ρsinθ化为直角坐标方程上式为即可得到答案.
解答:解:设P的极点坐标为(ρ,θ),
∴∠POM=α-θ,∠NOM=α+θ,
OM=ρcos(α-θ),PM=ρsin(α-θ),
ON=ρcos(α+θ),PN=ρsin(α+θ),
四边形PMON的面积
S=
OM•PM+
ON•PN=
[cos(α-θ)sin(α-θ)+cos(α+θ)sin(α+θ)]
依题意,动点P的轨迹的极坐标方程是:
[cos(α-θ)sin(α-θ)+cos(α+θ)sin(α+θ)]=c2
用倍角公式化简得
[sin2(α-θ)+sin2(α+θ)]=c2
用和差化积公式化简得
sin2αcos2θ=c2
即ρ2cos2θ=
.
用x=ρcosθ,y=ρsinθ化为直角坐标方程上式为
ρ2(cos2θ-sin2θ)=
.即x2-y2=
.
这个方程表示双曲线由题意,
动点P的轨迹是双曲线右面一支在∠AOB内的一部分.
∴∠POM=α-θ,∠NOM=α+θ,
OM=ρcos(α-θ),PM=ρsin(α-θ),
ON=ρcos(α+θ),PN=ρsin(α+θ),
四边形PMON的面积
S=
| 1 |
| 2 |
| 1 |
| 2 |
| ρ2 |
| 2 |
依题意,动点P的轨迹的极坐标方程是:
| ρ2 |
| 2 |
用倍角公式化简得
| ρ2 |
| 4 |
用和差化积公式化简得
| ρ2 |
| 2 |
即ρ2cos2θ=
| 2c2 |
| sin2α |
用x=ρcosθ,y=ρsinθ化为直角坐标方程上式为
ρ2(cos2θ-sin2θ)=
| 2c2 |
| sin2α |
| 2c2 |
| sin2α |
这个方程表示双曲线由题意,
动点P的轨迹是双曲线右面一支在∠AOB内的一部分.
点评:本题主要考查了根据极点坐标求轨迹的方程问题.此类题常涉及三角函数的问题,故应熟练记忆三角函数的公式.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥