题目内容
如图，已知△ABC是锐角三角形，SA⊥平面ABC，连结SB和SC，得到△SBC，过A作AO⊥平面SBC，O是垂足，求证：O不是△SBC的垂心．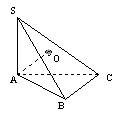
答案：
解析：
解析：
| 证明：用反证法
假设O是△SBC的垂心，则直线BO⊥SC， 又BO是AB在平面SBC的射影， ∴ SC⊥AB， ∵ AB⊥SA，∴ AB⊥平面SAC，AC 于是得到∠BAC=90°，与已知∠BAC是锐角矛盾 ∴ O不是△SBC的垂心．
|
练习册系列答案
相关题目
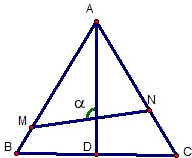如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的点，线段MN经过△ABC的中心G，设?MGA=a（
20、如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点．
如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BE的中点，求证：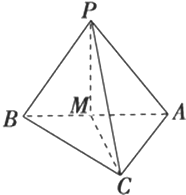
如图：已知△ABC是直角三角形，∠ACB=90°，M为AB的中点，PM⊥△ABC所在的平面，那么PA、PB、PC的大小关系是（ ）