题目内容
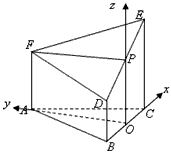
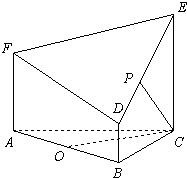
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,AF=2,CE=3,O为BC的中点,AO∥面EFD,
(Ⅰ)求BD的长;
(Ⅱ)求证:面EFD⊥面BCED;
(Ⅲ)求平面DEF与平面ACEF相交所成锐角二面角的余弦值.
(Ⅰ)求BD的长;
(Ⅱ)求证:面EFD⊥面BCED;
(Ⅲ)求平面DEF与平面ACEF相交所成锐角二面角的余弦值.
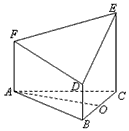
| 解:(Ⅰ)取ED的中点P,连接PO,PF, 则PO为梯形BCED的中位线, 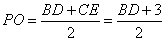 , ,又  , ,所以PO∥AF,所以A,O,P,F四点共面。 因为AO∥面EFD,且面AOPF∩面EFD=PF, 所以AO∥PF, 所以四边形AOPF为平行四边形,PO=AF=2, 所以BD=1。 (Ⅱ)由题意可知平面ABC⊥面BCED; 又AO⊥BC且 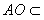 平面ABC, 平面ABC,所以AO⊥面BCED, 因为AO∥PF, 所以PF⊥面BCED, 又 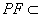 面EFD, 面EFD,所以面EFD⊥面BCED; (Ⅲ)以O为原点,OC,OA,OP所在直线分别为x,y,z轴, 建立空间直角坐标系, 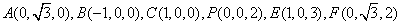 , ,设Q为AC的中点,则 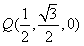 , ,易证:BQ⊥平面ACEF,平面ACEF的法向量为  , ,设平面DEF的法向量为 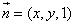 , ,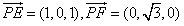 , ,由  得 得 ,所以 ,所以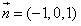 , ,所以 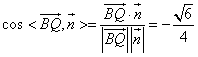 , ,所以平面DEF与平面ABC相交所成锐角二面角的余弦值为 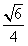 。 。 |
 |

练习册系列答案
相关题目
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点. 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( ) 如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点.
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点. 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥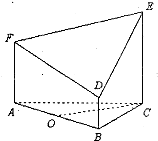 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.