题目内容
3. 如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.
如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.(1)求异面直线AD1和DC1所成角的余弦值.
(2)求点C到平面BC1D的距离.
分析 (1)由OO1∥AD1知,AD1和DC1所成角等于OO1和DC1所成的锐角或直角;
(2)设点C到平面BC1D的距离为h,则VC-BC1D=VC1-BCD,即用体积转化的方法求点到平面的距离.
解答 解:(1)由OO1∥AD1知,AD1和DC1所成角等于OO1和DC1所成的锐角或直角,
在△OO1D中,由题设可得,OD=$\frac{5}{2}$,O1D=2$\sqrt{2}$,OO1=$\frac{5}{2}$,
由余弦定理得,cos∠OO1D=$\frac{2\sqrt{5}}{5}$,
故AD1和DC1所成角的余弦值为:$\frac{2\sqrt{5}}{5}$;
(2)设点C到平面BC1D的距离为h,
则有:VC-BC1D=VC1-BCD,
其中,VC1-BCD=$\frac{1}{3}$•$\frac{BC•CD}{2}$•CC1=$\frac{1}{3}$•$\frac{3•4}{2}$•4=8,
在△BDC1中,BD=5,DC1=5,BC1=4$\sqrt{2}$,
所以,△BDC1的面积为$\frac{1}{2}$•$\sqrt{5^2-(2\sqrt{2})^2}$•4$\sqrt{2}$=2$\sqrt{34}$,
再由VC-BC1D=VC1-BCD得,$\frac{1}{3}$•2$\sqrt{34}$•h=8,
解得h=$\frac{2\sqrt{34}}{17}$,
即点C到平面BC1D的距离为:$\frac{2\sqrt{34}}{17}$.
点评 本题主要考查了异面直线所成的角的确定和求解,以及运用体积转化的方法求点到平面距离,属于中档题.

练习册系列答案
相关题目
 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分. 如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.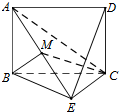 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.