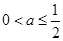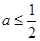题目内容
(本题满分13分)已知函数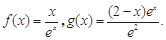
(1) 求函数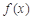 的极值;
的极值;
(2)求证:当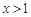 时,
时,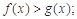
(3)如果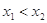 ,且
,且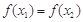 ,求证:
,求证:
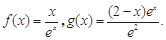
(1) 求函数
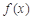 的极值;
的极值;(2)求证:当
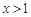 时,
时,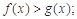
(3)如果
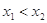 ,且
,且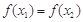 ,求证:
,求证:
(1) 当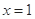 时,
时, 取得极大值
取得极大值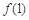 =
= ;
;
(2)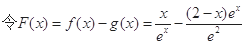 ,则只需证当
,则只需证当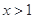 时,
时,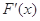 >0;
>0;
(3) 由⑵的结论知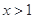 时,
时,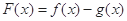 >0,∴
>0,∴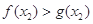 .
.
∵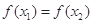 ,∴
,∴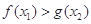 .
.
又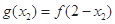 ,∴
,∴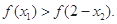 。
。
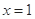 时,
时, 取得极大值
取得极大值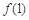 =
= ;
;(2)
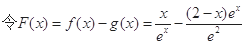 ,则只需证当
,则只需证当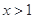 时,
时,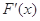 >0;
>0;(3) 由⑵的结论知
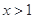 时,
时,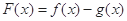 >0,∴
>0,∴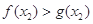 .
.∵
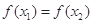 ,∴
,∴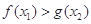 .
.又
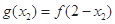 ,∴
,∴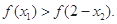 。
。试题分析:⑴∵
 =
=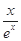 ,∴
,∴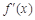 =
=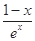 . 2分
. 2分令
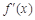 =0,解得
=0,解得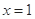 .
.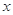 | 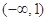 | 1 | 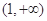 |
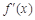 | + | 0 | - |
 | ↗ | 极大值 | ↘ |
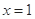 时,
时, 取得极大值
取得极大值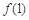 =
= . 4分
. 4分 ⑵证明:
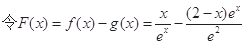 ,则
,则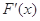 =
=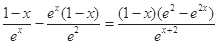 . 6分
. 6分 当
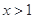 时,
时,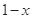 <0,
<0,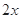 >2,从而
>2,从而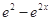 <0,
<0,∴
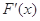 >0,
>0,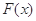 在
在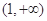 是增函数.
是增函数.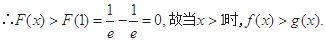 8分
8分⑶证明:∵
 在
在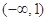 内是增函数,在
内是增函数,在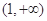 内是减函数.
内是减函数. ∴当
 ,且
,且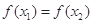 时,
时,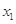 、
、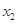 不可能在同一单调区间内.
不可能在同一单调区间内.∴
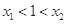 , 11分
, 11分由⑵的结论知
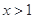 时,
时,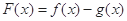 >0,∴
>0,∴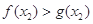 .
.∵
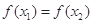 ,∴
,∴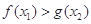 .
.又
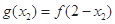 ,∴
,∴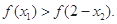 13分
13分点评:此题是个难题.主要考查函数与导数的综合应用能力,具体涉及到用导数来研究函数的单调性、极值等基础知识,考查运算能力及用函数思想分析解决问题的能力.做第三问的关键是:看出函数
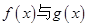 的关系,即
的关系,即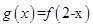 。
。
练习册系列答案
相关题目
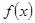 是
是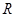 上的增函数,设
上的增函数,设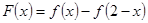 。
。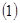 用定义证明:
用定义证明: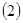 证明:如果
证明:如果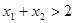 ,则
,则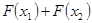 >0,(6分)
>0,(6分)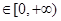 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( ) 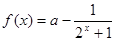 .
.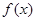 的单调性;
的单调性;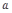 的值;
的值;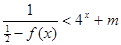 对
对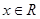 恒成立,求实数
恒成立,求实数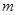 的取值范围.
的取值范围.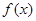 是定义在R上的奇函数,且满足
是定义在R上的奇函数,且满足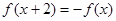 ,则
,则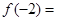 .
.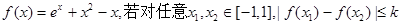 恒成立,则k的取值范围为 。
恒成立,则k的取值范围为 。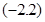 上的奇函数
上的奇函数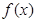 ,满足
,满足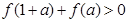 ,又当
,又当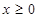 时,
时,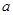 的取值范围。
的取值范围。 的值域是 .
的值域是 .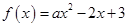 在
在 上是减函数,则
上是减函数,则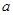 的取值范围是( )
的取值范围是( )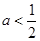
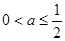
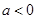 或
或