题目内容
设函数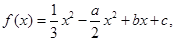 其中
其中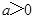 ,曲线
,曲线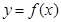 在点
在点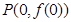 处的切线方程为
处的切线方程为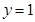 .
.
(I)确定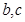 的值;
的值;
(II)设曲线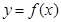 在点
在点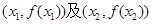 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当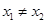 时,
时,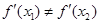 ;
;
(III)若过点(0,2)可作曲线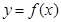 的三条不同切线,求
的三条不同切线,求 的取值范围.
的取值范围.
(I)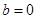 ,
, ;(II)详见试题解析;(III)
;(II)详见试题解析;(III) 的取值范围是
的取值范围是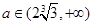 .
.
解析试题分析:(I)根据导数的几何意义,首先对函数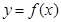 求导,可得
求导,可得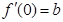 ,由已知:曲线
,由已知:曲线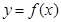 在点
在点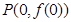 处的切线方程为
处的切线方程为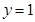 ,从而可得
,从而可得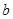 的值及
的值及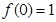 ,又
,又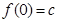 ,故得
,故得 ;(II)先利用导数的几何意义,求出
;(II)先利用导数的几何意义,求出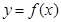 在点
在点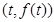 处的切线方程为
处的切线方程为 ,而点
,而点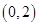 在切线上,所以
在切线上,所以 ,化简即得
,化简即得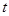 满足的方程为
满足的方程为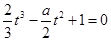 ,下面利用反证法明当
,下面利用反证法明当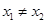 时,
时,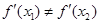 ;(III)由(II)知,过点
;(III)由(II)知,过点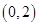 可作
可作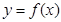 的三条切线,等价于方程
的三条切线,等价于方程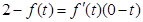 有三个相异的实根,即等价于方程
有三个相异的实根,即等价于方程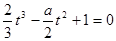 有三个相异的实根.构造函数
有三个相异的实根.构造函数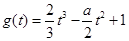 ,利用导数求函数
,利用导数求函数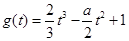 的极大值、极小值,只要
的极大值、极小值,只要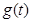 的极大值与极小值异号即可,解这个不等式组即可求得
的极大值与极小值异号即可,解这个不等式组即可求得 的取值范围.
的取值范围.
试题解析:(I)由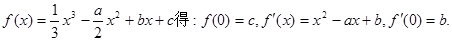 又由曲线
又由曲线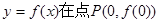 处的切线方程为
处的切线方程为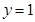 ,得
,得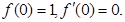 故
故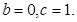
(II) 处的切线方程为
处的切线方程为 ,而点
,而点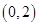 在切线上,所以
在切线上,所以 ,化简得
,化简得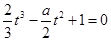 ,即
,即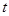 满足的方程为
满足的方程为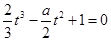 .
.
下面用反证法证明:假设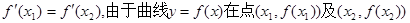 处的切线都过点
处的切线都过点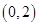 ,则下列等式成立.
,则下列等式成立.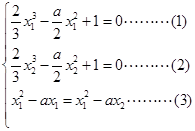
由(3)得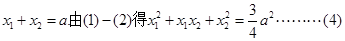
又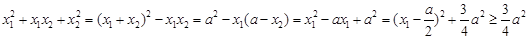 ,故由(4)得
,故由(4)得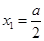 ,此时
,此时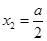 与
与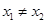 矛盾,
矛盾,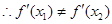 .
.
(III)由(II)知,过点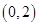 可作
可作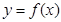 的三条切线,等价于方程
的三条切线,等价于方程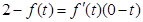 有三个相异的实根,即等价于方程
有三个相异的实根,即等价于方程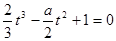 有三个相异的实根.
有三个相异的实根.
设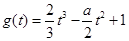 ,则
,则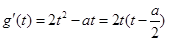 ,由于
,由于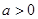 ,故有
,故有
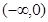
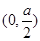
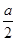
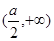
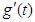

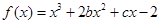 的图象在与
的图象在与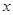 轴交点处的切线方程是
轴交点处的切线方程是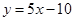 .
. 的解析式;
的解析式;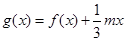 ,若
,若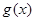 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数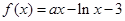 .
.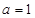 时,求函数
时,求函数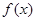 在点
在点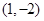 处的切线方程;
处的切线方程;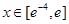 上的图像与直线
上的图像与直线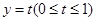 恒有两个不同交点,求实数
恒有两个不同交点,求实数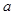 的取值范围.
的取值范围. .
.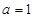 时,求曲线
时,求曲线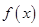 在
在 处的切线方程;
处的切线方程;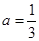 时,求函数
时,求函数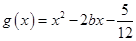 ,若对于
,若对于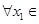 [1,2],
[1,2], [0,1],使
[0,1],使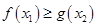 成立,求实数
成立,求实数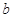 的取值范围.
的取值范围.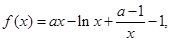 试讨论
试讨论 的单调性.
的单调性.
 的单调区间;
的单调区间;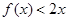 在
在 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;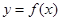 在
在 上值域是
上值域是 ,求实数
,求实数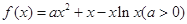 .
.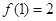 ,且在定义域内
,且在定义域内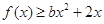 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;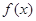 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;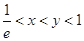 时,试比较
时,试比较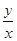 与
与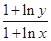 的大小.
的大小.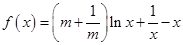 ,(其中常数
,(其中常数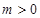 ).
).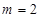 时,求
时,求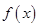 的极大值;
的极大值;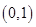 上的单调性;
上的单调性;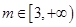 时,曲线
时,曲线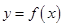 上总存在相异两点
上总存在相异两点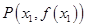 、
、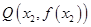 ,使得曲线
,使得曲线 、
、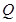 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围. 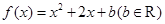 .
. 的值域为
的值域为 .求关于
.求关于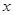 的不等式
的不等式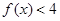 的解集;
的解集;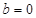 时,
时,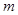 为常数,且
为常数,且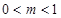 ,
,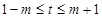 ,求
,求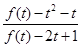 的最小值.
的最小值.