题目内容
已知函数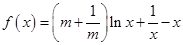 ,(其中常数
,(其中常数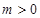 ).
).
(1)当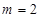 时,求
时,求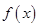 的极大值;
的极大值;
(2)试讨论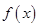 在区间
在区间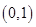 上的单调性;
上的单调性;
(3)当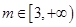 时,曲线
时,曲线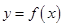 上总存在相异两点
上总存在相异两点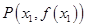 、
、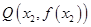 ,使得曲线
,使得曲线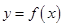 在点
在点 、
、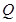 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
(1)函数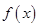 的极大值为
的极大值为 ;(2)详见解析;(3)
;(2)详见解析;(3) 的取值范围是
的取值范围是 .
.
解析试题分析:(1)将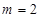 代入函数
代入函数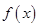 的解析式,利用导数求出函数
的解析式,利用导数求出函数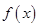 的极大值即可;(2)先求出导数
的极大值即可;(2)先求出导数 ,并求出方程
,并求出方程 的两根
的两根 和
和 ,对这两根的大小以及两根是否在区间
,对这两根的大小以及两根是否在区间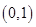 进行分类讨论,并借助导数正负确定函数
进行分类讨论,并借助导数正负确定函数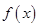 在区间
在区间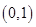 上的单调区间;(3)先利用函数
上的单调区间;(3)先利用函数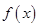 在
在 、
、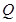 两点处的切线平行得到
两点处的切线平行得到 ,通过化简得到
,通过化简得到 ,利用基本不等式转化为
,利用基本不等式转化为 在
在 上恒成立,于是有
上恒成立,于是有 ,进而求出
,进而求出 的取值范围.
的取值范围.
试题解析:(1)当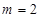 时,
时, ,定义域为
,定义域为 ,
,
所以 ,
,
令 ,解得
,解得 或
或 ,列表如下:
,列表如下:

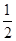









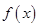
减 极小值 
增 极大值  练习册系列答案
练习册系列答案
课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案


课堂作业广西教育出版社系列答案
相关题目
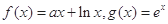 .
.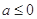 时,求
时,求 的单调区间
的单调区间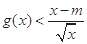 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;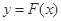 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数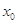 ,称
,称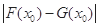 的值为两函数在
的值为两函数在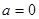 时,函数
时,函数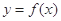 和
和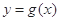 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。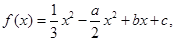 其中
其中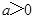 ,曲线
,曲线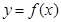 在点
在点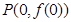 处的切线方程为
处的切线方程为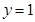 .
.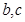 的值;
的值;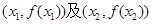 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当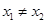 时,
时,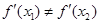 ;
; 的取值范围.
的取值范围.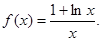
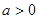 且函数
且函数 在区间
在区间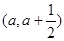 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;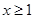 时,不等式
时,不等式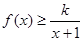 恒成立,求实数
恒成立,求实数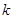 的取值范围.
的取值范围.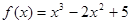 的定义域为区间
的定义域为区间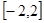 .
. 的极大值与极小值;
的极大值与极小值;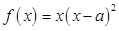 ,
,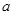 是大于零的常数.
是大于零的常数.  时,求
时,求 的极值;
的极值; 上为单调递增,求实数
上为单调递增,求实数 上存在一点
上存在一点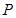 ,使得曲线
,使得曲线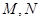 ,且
,且 成立.
成立.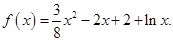
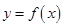 的单调区间;
的单调区间;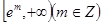 上有零点,求
上有零点,求 的最大值.
的最大值.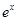 +3
+3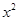 -ax.
-ax.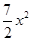 +ax+1在x≥
+ax+1在x≥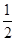 时恒成立,试求实数a的取值范围.
时恒成立,试求实数a的取值范围.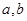 是正实数,设函数
是正实数,设函数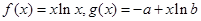 。
。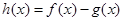 ,求
,求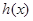 的单调区间;
的单调区间;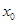 ,使
,使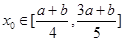 且
且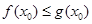 成立,求
成立,求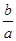 的取值范围。
的取值范围。