题目内容
11.方程3x2+y2=3x-2y的非负整数解(x,y)的组数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 要求方程3x2+y2=3x-2y的非负整数解(x,y)的组数,进行简单的化简得3(x-$\frac{1}{2}$)2+(y+1)2=$\frac{7}{4}$,然后进行讨论,可以得到结论.
解答 解:3x2+y2=3x-2y,
3x2+y2-3x+2y=0,
3(x-$\frac{1}{2}$)2+(y+1)2=$\frac{7}{4}$,
当x=0时,y=0,即(0,0),
当x=1时,y=0,即(1,0),
当x=2时,y无解.
当x≥2时,y均无解,
综上所述方程3x2+y2=3x-2y的非负整数解(x,y)的组数为2.
故选C.
点评 本题考查了二次二次方程的整数根的问题,属于中档题.

练习册系列答案
相关题目
1.函数$f(x)=sin2x+\sqrt{3}cos2x$的最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
2.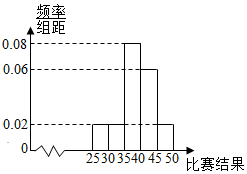 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
其频率分布直方图为:
(1)求人数统计表中的a和b的值;
(2)根据频率分布直方图,估计该项比赛结果的中位数;
(3)用分层抽样的方法从第1,2,3组中共抽取6人,再从这6人中随机抽取2人参加上一级比赛活动,求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率.
 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(1)求人数统计表中的a和b的值;
(2)根据频率分布直方图,估计该项比赛结果的中位数;
(3)用分层抽样的方法从第1,2,3组中共抽取6人,再从这6人中随机抽取2人参加上一级比赛活动,求参加上一级比赛活动中至少有1人的比赛结果在第3组的概率.
6.设D为不等式组$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 2x+y-3≤0\end{array}\right.$表示的平面区域,圆C:(x-5)2+y2=1上的点与区域D上的点之间的距离的取值范围是( )
| A. | [$\frac{5\sqrt{2}}{2}$-1,$\sqrt{34}+1$) | B. | [$\sqrt{17}-1$,$\sqrt{34}+1$] | C. | [$\sqrt{17}$,$\sqrt{34}$] | D. | [$\sqrt{17}$-1,$\sqrt{34}$-1] |
3.已知直线x-9y-8=0与曲线C:y=x3-px2+3x相交于A,B,且曲线C在A,B处的切线平行,则实数p的值为( )
| A. | 4 | B. | 4或-3 | C. | -3或-1 | D. | -3 |
1.已知圆C:x2+y2=1,在线段AB:x-y+2=0(-2≤x≤3)上任取一点M,过点M作圆C切线,求“点M与切点的距离不大于3”的概率P为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{5}$ |
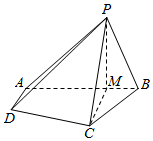 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.