题目内容
20.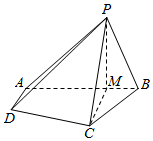 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.(1)证明:平面PAB⊥平面ABCD;
(2)求平面ABCD与平面PCD所成的锐二面角的余弦值.
分析 (1)由已知条件推导出PM⊥AB,从而得到PM⊥面ABCD,由此能证明面PAB⊥面ABCD.
(2)根据二面角的定义,作出二面角的平面角,结合三角形的边角关系进行求解即可.
解答 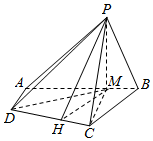 (1)证明:∵AB=2PB=4BM,∴PM⊥AB,
(1)证明:∵AB=2PB=4BM,∴PM⊥AB,
又∵PM⊥CD,且AB∩CD,
∴PM⊥面ABCD,
∵PM?面PAB.∴面PAB⊥面ABCD.
(2)过点M作MH⊥CD,连结HP,
∵PM⊥CD,且PM∩MH=M,
∴CD⊥平面PMH,
∴CD⊥PH,
则∠PHM是二面角平面PCD与平面ABCD所成角的平面角,
在四棱锥P-ABCD中,设AB=2t,
则DM=$\frac{\sqrt{13}}{2}$t,PM=$\frac{\sqrt{3}}{2}$t,MH=$\frac{7\sqrt{5}}{10}$t,
∴PH=$\frac{4\sqrt{5}}{5}$t,
从而cos∠PHM=$\frac{HM}{PH}$=$\frac{\frac{7\sqrt{5}}{10}t}{\frac{4\sqrt{5}}{5}t}$=$\frac{7}{8}$,
即平面ABCD与平面PCD所成的锐二面角的余弦值是$\frac{7}{8}$.
点评 本题考查平面与平面垂直的证明,考查二面角的求法,解题时要认真审题,注意空间思维能力的培养.利用定义法作出二面角的平面角是解决本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
11.方程3x2+y2=3x-2y的非负整数解(x,y)的组数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.已知集合S={1,2,a},T={2,3,4,b},若S∩T={1,2,3},则a-b=( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
12.2015年12月27日全国人大常委会会议通过了关于修教口与计划生育法的决定,“全面二孩”从2016年元旦起开给实施.A市妇联为了解该市市民对“全面二孩”政策的态度,随机抽取了男性市民45人、女性市民55人进行调查,得到以下2×2列联表.
(1)根据以上数据,能否有90%的把握认为A市市民“支持全面二孩”与“性别”有关?
(2)现从参与调查的女性用户中按分层抽样的方法选出11名发放礼品,在所抽取的11人中分别求出“支持”和“不支持”态度的人数;
(3)将上述调查所得到的频率视为概率,现在从A市所有市民中,采取随机抽样的方法抽取3位市民进行长期跟踪调查,记被抽取的3位市民中持“支持”态度人数为X.
①求X的分布列;
②求X的数学期望E(X)和方差D(X).
附表及公式:
K2=$\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 支持 | 反对 | 合计 | |
| 男性 | 30 | 15 | 45 |
| 女性 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)现从参与调查的女性用户中按分层抽样的方法选出11名发放礼品,在所抽取的11人中分别求出“支持”和“不支持”态度的人数;
(3)将上述调查所得到的频率视为概率,现在从A市所有市民中,采取随机抽样的方法抽取3位市民进行长期跟踪调查,记被抽取的3位市民中持“支持”态度人数为X.
①求X的分布列;
②求X的数学期望E(X)和方差D(X).
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
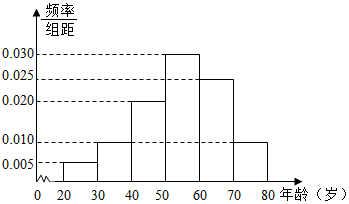 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.