题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 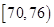 | 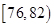 | 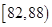 | 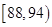 | 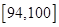 |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
(Ⅰ)元件A为正品的概率为 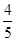 ,元件B为正品的概率为
,元件B为正品的概率为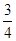
(Ⅱ)(i)
(ii)所以 的分布列为:
的分布列为:
150 90 30 -30 


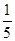
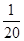

解析试题分析:(Ⅰ)用频率估计概率值;
(Ⅱ)设出随机变量,确定随机变量的所有可能取值,求出各个取值的概率,列出概率分布表,从而得出答案.
试题解析:(Ⅰ)由题可知 元件A为正品的概率为 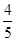 ,元件B为正品的概率为
,元件B为正品的概率为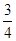 。 2分
。 2分
(Ⅱ)(i)设生产的5件元件中正品件数为 ,则有次品5
,则有次品5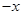 件,由题意知
件,由题意知 得到
得到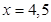 ,设“生产5件元件B所获得的利润不少于300元”为事件
,设“生产5件元件B所获得的利润不少于300元”为事件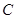 ,则
,则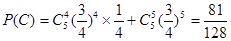 。 6分
。 6分
(ii)随机变量 的所有取值为150,90,30,-30,
的所有取值为150,90,30,-30,
则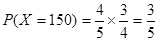 ,
, ,
,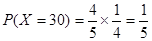 ,
,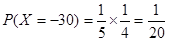 ,
,
所以 的分布列为:
的分布列为:
10分
150 90 30 -30 


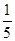
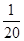
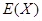
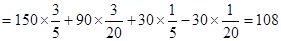 12分
12分
考点:1概率;2、随机变量的分布率;3、数学期望.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望
 .
.  ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先. ,
, ,点
,点 的坐标为
的坐标为 .
. 时,点
时,点 的概率;
的概率; 时,点
时,点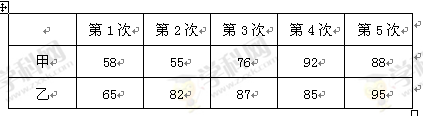
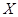 ,求随机变量
,求随机变量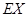 .
. 三个区中抽取6个工厂进行调查.已知
三个区中抽取6个工厂进行调查.已知 区的概率.
区的概率. 顶点
顶点 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
 的概率
的概率 ;
; 表示跳到过
表示跳到过 .
. ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是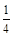 .
. 表示回答该题正确的人数,求
表示回答该题正确的人数,求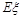 .
.