题目内容
电子蛙跳游戏是:青蛙第一步从如图所示的正方体 顶点
顶点 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
(1)求跳三步跳到 的概率
的概率 ;
;
(2)青蛙跳五步,用 表示跳到过
表示跳到过 的次数,求随机变量
的次数,求随机变量 的概率分布及数学期望
的概率分布及数学期望 .
.
 ;(2)期望为
;(2)期望为 , 概率分布表
, 概率分布表X 0 1 2 p 


解析试题分析:我们把正方体的八个顶点分类,让每一步跳显得很明显,将 标为0,从
标为0,从 一步能跳到的点
一步能跳到的点 标为1,接下来
标为1,接下来 标为2,
标为2, 标为3,从A跳到B记为01,从B跳到B1再跳到A1记为121,
标为3,从A跳到B记为01,从B跳到B1再跳到A1记为121,
跳三步到 就是0123,从0到1与3与2的概率都是1,从1到0与2到3的概率都是
就是0123,从0到1与3与2的概率都是1,从1到0与2到3的概率都是 ,从1到2与2到1的概率都是
,从1到2与2到1的概率都是 ,(1)就是求
,(1)就是求 ,(2)跳五步跳到过
,(2)跳五步跳到过 的次数只能是0,1,2三种情形,数学期望
的次数只能是0,1,2三种情形,数学期望 .
.
试题解析:将A标示为0,A1、B、D标示为1,B1、C、D1标示为2,C1标示为3,从A跳到B记为01,从B跳到B1再跳到A1记为121,其余类推.从0到1与从3到2的概率为1,从1到0与从2到3的概率为 ,从1到2与从2到1的概率为
,从1到2与从2到1的概率为 .
.
(1)P=P(0123)=1


 =
= ; 4′
; 4′
(2)X=0,1,2.P(X=1)=P(010123)+P(012123)+P(012321)
=1

 1
1


 +1
+1






 +1
+1



 1
1

= ,P(X=2)=P(012323)=1
,P(X=2)=P(012323)=1



 1
1
 =
= ,
,
P(X=0)=1-P(X=1)-P(X=2)=
或P(X=0)=P(010101)+P(010121)+P(012101)+P(012121)
=1

 1
1

 1+1
1+1

 1
1


 +1
+1





 1+1
1+1






练习册系列答案
相关题目
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 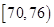 | 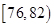 | 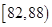 | 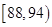 |  |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望  有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 元,正确回答问题
元,正确回答问题 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生. 、
、 、
、 。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率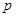 .
.

 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求