题目内容
已知
，
，点
的坐标为
.
（1）求当
时，点满足
的概率；
（2）求当
时，点满足的概率.
（1）
；（2）
.
解析试题分析：（1）这是几何概型的概率计算问题，先确定总区域即不等式组
所表示的平面区域的面积
，后确定不等式组
所表示的平面区域的面积
，最后根据几何概型的概率计算公式
计算即可；（2）先计算出满足不等式组所包含的整点的个数
，后确定不等式组所包含的整点的个数
，最后由
即可得到所求的概率.
试题解析：（1）点所在的区域为正方形
的内部（含边界） （1分）
满足
的点的区域为以
为圆心，2为半径的圆面（含边界） （3分）
所求的概率
（5分）
（2）满足
，且，的整点有25个 （8分）
满足，且的整点有6个 （11分）所求的概率
（12分）.
考点：1.古典概率；2.几何概型的概率.
练习册系列答案
口算题天天练系列答案
相关题目
，科目B每次考试成绩合格的概率均为
.假设各次考试成绩合格与否均互不影响.
，求某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙，已知从城市甲到城市乙只有两条公路，且运费由厂商承担．若厂商恰能在约定日期(×月×日)将牛奶送到，则城市乙的销售商一次性支付给牛奶厂20万元；若在约定日期前送到，每提前一天销售商将多支付给牛奶厂1万元；若在约定日期后送到，每迟到一天销售商将少支付给牛奶厂1万元．为保证牛奶新鲜度，汽车只能在约定日期的前两天出发，且只能选择其中的一条公路运送牛奶，已知下表内的信息：
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 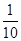 | 1.6 |
| 公路2 | 1 | 4 | 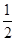 | 0.8 |
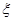(单位：万元)，求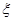的分布列和数学期望
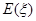；（II）如果你是牛奶厂的决策者，你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多？
(注：毛收入＝销售商支付给牛奶厂的费用－运费)
店经销
三种排量的汽车，其中
种排量汽车的概率；
，求
的分布列及数学期望．生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为
次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：
| 测试指标 |  |  |  |  |  |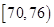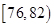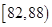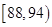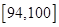
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
（Ⅱ）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下；
（i）求生产5件元件B所获得的利润不少于300元的概率；
（ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．
有三个选项，问题
有四个选项，但都只有一个选项是正确的，正确回答问题
元，正确回答问题
元，活动规定：参与者可任意选择回答问题的顺序，如果第一个问题回答正确，则继续答题，否则该参与者猜奖活动终止，假设一个参与者在回答问题前，对这两个问题都很陌生.