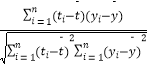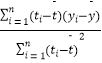Question

【题目】已知f（x）= ，g（x）= ．
（1）当1≤x＜2时，求g（x）；
（2）当x∈R时，求g（x）的解析式，并画出其图象；

（3）求方程xf[g（x）]=2g[f（x）]的解．

Answer 1

【答案】
（1）解：当1≤x＜2时，x﹣1≥0，x﹣2＜0，

故

（2）解：由（1）知，当1≤x＜2时， ．

当x＜1时，x﹣1＜0，x﹣2＜0，故 ．

当x≥2时，x﹣1＞0，x﹣2≥0，故 ．

所以当x∈R时，g（x）的解析式为 ．

其函数图象为

（3）解：∵g（x）＞0，∴f[g（x）]=2，x∈R

所以方程xf[g（x）]=2g[f（x）]为

解得

【解析】（1）根据自变量的范围选择对应的解析式代入求解，（2）先求出解析式，再画函数图象（分段函数），（3）先将方程化简一下，再求解．