ћвƒњƒЏ»Ё
°Њћвƒњ°њ»зЌЉ «ќ“єъ2008ƒк÷Ѕ2014ƒк…ъїојђїшќёЇ¶їѓі¶јнЅњ£®µ•ќї£Ї“Џґ÷£©µƒ’џѕяЌЉ 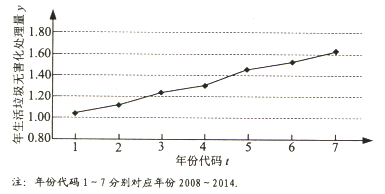
£®Ґс£©”…’џѕяЌЉњі≥ц£ђњ…”√ѕя–‘їЎєйƒ£–ЌƒвЇѕy”лtµƒєЎѕµ£ђ«л”√ѕаєЎѕµ эЉ”“‘Ћµ√ч£ї
£®Ґт£©љ®ЅҐyєЎ”ЏtµƒїЎєйЈљ≥ћ£®ѕµ эЊЂ»Јµљ0.01£©£ђ‘§≤в2017ƒкќ“єъ…ъїојђїшќёЇ¶їѓі¶јнЅњ£Ѓ
≤ќњЉ эЊЁ£Ї ![]() =9.32£ђ
=9.32£ђ ![]() yi=40.17£ђ
yi=40.17£ђ ![]() =0.55£ђ
=0.55£ђ ![]() °÷2.646£Ѓ
°÷2.646£Ѓ
≤ќњЉєЂ љ£ЇѕаєЎѕµ эr= 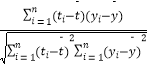 їЎєйЈљ≥ћ
їЎєйЈљ≥ћ ![]() =
= ![]() +
+ ![]() t ÷––±¬ ЇЌљЎЊаµƒ„о–°ґю≥ЋєјЉ∆єЂ љЈ÷±рќ™£Ї
t ÷––±¬ ЇЌљЎЊаµƒ„о–°ґю≥ЋєјЉ∆єЂ љЈ÷±рќ™£Ї ![]() =
= 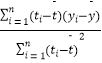 £ђ
£ђ ![]() =
= ![]() ©Б
©Б ![]() £Ѓ
£Ѓ
°Њір∞Є°њљв£Ї£®Ґс£©”…’џѕяЌЉњі≥ц£ђy”лt÷ЃЉдіж‘Џљѕ«њµƒ’эѕаєЎєЎѕµ£ђ°я ![]() =9.32£ђ
=9.32£ђ ![]() yi=40.17£ђ
yi=40.17£ђ 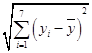 =0.55£ђ
=0.55£ђ
°аr°÷ ![]() °÷0.993£ђ
°÷0.993£ђ
°я0.993£Њ0.75£ђ
є y”лt÷ЃЉдіж‘Џљѕ«њµƒ’эѕаєЎєЎѕµ£ї
£®Ґт£©”… ![]() °÷1.331Љ∞£®Ґс£©µ√
°÷1.331Љ∞£®Ґс£©µ√ ![]() =
= ![]() °÷0.103£ђ
°÷0.103£ђ![]() =1.331©Б0.103°Ѕ4=0.92£Ѓ
=1.331©Б0.103°Ѕ4=0.92£Ѓ
Ћщ“‘£ђyєЎ”ЏtµƒїЎєйЈљ≥ћќ™£Ї ![]() =0.92+0.10t£Ѓ
=0.92+0.10t£Ѓ
љЂ2017ƒкґ‘”¶µƒt=10іъ»лїЎєйЈљ≥ћµ√£Ї ![]() =0.92+0.10°Ѕ10=1.92
=0.92+0.10°Ѕ10=1.92
Ћщ“‘‘§≤в2017ƒкќ“єъ…ъїојђїшќёЇ¶їѓі¶јнЅњљЂ‘Љ1.92“Џґ÷
°Њљвќц°њ£®Ґс£©”…’џѕяЌЉњі≥ц£ђy”лt÷ЃЉдіж‘Џљѕ«њµƒ’эѕаєЎєЎѕµ£ђљЂ“—÷™ эЊЁіъ»лѕаєЎѕµ эЈљ≥ћ£ђњ…µ√ір∞Є£ї£®Ґт£©ЄщЊЁ“—÷™÷–µƒ эЊЁ£ђ«у≥цїЎєйѕµ э£ђњ…µ√їЎєйЈљ≥ћ£ђ2017ƒкґ‘”¶µƒt÷µќ™10£ђіъ»лњ…‘§≤в2017ƒкќ“єъ…ъїојђїшќёЇ¶їѓі¶јнЅњ£Ѓ

 ѕ∞ћвЊЂ—°ѕµЅ–ір∞Є
ѕ∞ћвЊЂ—°ѕµЅ–ір∞Є