题目内容
用向量方法证明对角线互相平分的四边形是平行四边形.
答案:
解析:
提示:
解析:
|
答案:已知:如图所示,在四边形ABCD中,对角线AC与BD交于O,且AO=OC,DO=OB.
求证:四边形ABCD是平行四边形. 证明:根据向量加法的三角形法则,有 即AB与DC平行且相等.∴四边形ABCD是平行四边形. 思路分析:要证四边形是平行四边形,只需证一组对边平行且相等.根据向量相等的意义,只需证其一组对边对应向量相等即可.此问题是纯文字叙述的问题,首先应转化为符号语言描述. |
提示:
|
用向量法解决应用问题的步骤为:(1)将应用问题中的量抽象成向量;(2)化归为向量问题,进行向量运算;(3)将向量问题还原为应用问题. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


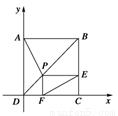
 在正方形ABCD中,P是对角线BD上一点,E、F分别在边BC、CD上,且四边形PECF为矩形,用向量方法证明:
在正方形ABCD中,P是对角线BD上一点,E、F分别在边BC、CD上,且四边形PECF为矩形,用向量方法证明: