题目内容

设集合Z划分为两两不相交的子集A1，A2，…，An，又划分为两两不相交的子集B1，B2，…，Bn．已知任意两个不相交子集Ai与Bj的并集Ai∪Bj至少含有n个元素，1≤i，j≤n．求证：集合Z中的元素个数至少为
n2
2
，它能否等于
n2
2
？
考点：元素与集合关系的判断
专题：集合
分析：若设子集Ai最少含有nA个元素，则集合Z中每个子集都含nA个元素时，集合Z所含元素最少，最少为n•nA个元素；同理，若设子集Bj最少含nB个元素，则集合Z最少含n•nB个元素，所以集合Z最少含有元素：
n•nA+n•nB
2
=
n2
2
个．并且能取到
n2
2
，这时任意子集Ai含有相同的元素，这就需要集合Z含有的元素个数能够被n整除．
解答： 解：设集合Ai至少含nA个元素，集合Bj至少含nB个元素，集合Z至少含有m个元素，则：nA+nB=n；
∴m=
n•nA+n•nB
2
=
n2
2
，即集合Z中的元素至少为
n2
2
，并且当m被n整除时，它能等于
n2
2
．
点评：只要读懂题意，这道题是不难做的，这需要理解并集的概念，交集的概念，并且弄清怎样让集合Z含有的元素最少．
练习册系列答案
相关题目
如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=2，点E是SD的中点．
（Ⅰ）试建立适当的坐标系；并写出点A，C，E，B的坐标．
（Ⅱ）求异面直线AC与BE夹角的大小．
在等差数列{an}和等比数列{bn}中，a1=1，b1=2，bn＞0（n∈N*），且b1，a2，b2成等差数列，a2，b2，a3+2成等比数列，数列{bn}的前n项和为Sn．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）若Sn+an＞m对任意的正整数n恒成立，求常数m的取值范围．
在△ABC中，∠A、B、C所对的边分别是a、b、c，且满足a2-2bccosA=（b+c）2
（1）求∠A的大小；
（2）若a=3，求△ABC周长的取值范围．
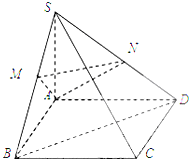如图，在四棱锥S-ABCD中，SA⊥平面ABCD，底ABCD为正方形M、N分别
为SB、SD的中点．求证：
（1）MN∥平面ABCD；
（2）CB⊥平面SAB．
某校举办一场篮球投篮选拔比赛，比赛的规则如下：每个选手先后在二分区、三分区和中场跳球区三个位置各投一球，只有当前一次球投进后才能投下一次，三次全投进就算胜出，否则即被淘汰．已知某选手在二分区投中球的概率为
4
5
，在三分区投中球的概率为
3
5
，在中场跳球区投中球的概率为
2
5
，且在各位置投球是否投进互不影响．
（Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在比赛中投球的个数记为ξ，求随机变量ξ的分布列与数学期望Eξ．（注：本小题结果可用分数表示）
数列{an}定义如下：a1=1，对于每个n∈N*，a4n-3，a4n-2，a4n-1构成公差为1的等差数列，而a4n-1，a4n，a4n+1构成公比为2的等比数列．
（1）求a2，a6的值以及a4n-2（n∈N*）的通项公式；
（2）若bn=（a1+a2+a3）+（a5+a6+a7）+…+（a4n-3+a4n-2+a4n-1），在数列{bn}中是否存在不同的三项，使得此三项能成为某三角形的三条边长？若能，求出这三项；若不能，请说明理由．
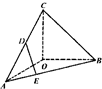如图，在四面体ABCD中，OC⊥OA，OC⊥OB，∠AOB=120°，且OA=OB=OC=
3
，D是AC的中点，点E在AB上，AB=3AE．
（Ⅰ）求证：AO⊥DE；
（Ⅱ）求二面角O-AC-B的余弦值．
画出如图所示程序相应的程序框图．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网