题目内容
用[x]表示不超过x的最大整数,例如[-2.5]=-3,[2.5]=2,设函数f(x)=[x[x]].
(1)f(3.6)= ;
(2)若函数f(x)的定义域是[0,n),n∈N+,则其值域中元素个数为 .
(1)f(3.6)=
(2)若函数f(x)的定义域是[0,n),n∈N+,则其值域中元素个数为
考点:函数的值,元素与集合关系的判断
专题:函数的性质及应用,点列、递归数列与数学归纳法
分析:本题(1)利用取整函数的规定,求出[3.6]的值,再求出[3.6[3.6]]的值,得到本题结论;(2)利用取整函数的规定,根据x∈[0,n),找出其函数值的取值规律,求出值域中元素个数,得到本题结论.
解答:
解:(1)∵函数f(x)=[x[x]],
∴f(3.6)=[3.6[3.6]]=[3.6×3]=[10.8]=10.
(2)∵函数f(x)的定义域是[0,n),n∈N+,
∴当0≤x<1时,[x]=0,f(x)=[x[x]]=[x×0]=[0]=0,函数值有1个,
当1≤x<2时,[x]=1,f(x)=[x[x]]=[x×1]=[x]=1,函数值有1个,
当2≤x<3时,4≤2x<6
[x]=2,f(x)=[x[x]]=[x×2]=[2x],能取到4,5,函数值有2个,
当3≤x<4时,9≤3x<12,
[x]=3,f(x)=[x[x]]=[x×3]=[3x],能取到9,10,11,函数值有3个,
当4≤x<5时,16≤4x<20,
[x]=4,f(x)=[x[x]]=[x×4]=[4x],能取到16,17,18,19,函数值有4个,
…
当n-1≤x<n时,(n-1)2≤(n-1)x<n(n-1),
[x]=n-1,f(x)=[x[x]]=[x×(n-1)]=[(n-1)x],能取到(n-1)2,(n-1)2+1,(n-1)2+2,…,n(n-1)-1,函数值有n-1个,
∴值域中元素个数为:1+1+2+3+…+(n-1)=
.
故答案为:
.
∴f(3.6)=[3.6[3.6]]=[3.6×3]=[10.8]=10.
(2)∵函数f(x)的定义域是[0,n),n∈N+,
∴当0≤x<1时,[x]=0,f(x)=[x[x]]=[x×0]=[0]=0,函数值有1个,
当1≤x<2时,[x]=1,f(x)=[x[x]]=[x×1]=[x]=1,函数值有1个,
当2≤x<3时,4≤2x<6
[x]=2,f(x)=[x[x]]=[x×2]=[2x],能取到4,5,函数值有2个,
当3≤x<4时,9≤3x<12,
[x]=3,f(x)=[x[x]]=[x×3]=[3x],能取到9,10,11,函数值有3个,
当4≤x<5时,16≤4x<20,
[x]=4,f(x)=[x[x]]=[x×4]=[4x],能取到16,17,18,19,函数值有4个,
…
当n-1≤x<n时,(n-1)2≤(n-1)x<n(n-1),
[x]=n-1,f(x)=[x[x]]=[x×(n-1)]=[(n-1)x],能取到(n-1)2,(n-1)2+1,(n-1)2+2,…,n(n-1)-1,函数值有n-1个,
∴值域中元素个数为:1+1+2+3+…+(n-1)=
| n2-n+2 |
| 2 |
故答案为:
| n2-n+2 |
| 2 |
点评:本题考查了取整函数的定义及其应用,本题有一定的难度,属于中档题.

练习册系列答案
相关题目
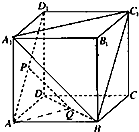 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P、Q分别是AD1、BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P、Q分别是AD1、BD的中点.