题目内容

【题目】如图，已知双曲线C： =1（a＞0，b＞0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ= ，且 |，则双曲线C的离心率为（ ）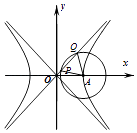
A.
B.
C.
D.

【答案】D
【解析】解：∵∠PAQ= ，AP=AQ， ∴△PAQ是等边三角形，
设圆A的半径为r，
过A作AB⊥PQ，垂足为B，则B为PQ的中点，
∴PB= r，AB= r，
∵OQ=3OP，∴OB=2OP=r，
∴tan∠AOB= = ，
又渐近线方程为y= ，
∴ = ，即b= a，
∴e= = = ，
解法二：由于双曲线的离心率e＞1，排除A，B，C，
故选D．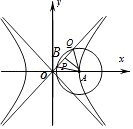

过A作AB⊥PQ，设圆A半径为r，三角形APQ是等边三角形，用r表示出OB，AB计算渐近线的斜率，从而得出a，b的关系得出离心率．

练习册系列答案
相关题目

【题目】如图，在正三棱柱ABC﹣A1B1C1中，已知D，E分别为BC，B1C1的中点，点F在棱CC1上，且EF⊥C1D．求证：

（1）直线A1E∥平面ADC1；
（2）直线EF⊥平面ADC1 ．

【题目】已知点F1（﹣1，0），F2（1，0），动点M到点F2的距离是 ，线段MF1的中垂线交线段MF2于点P． （Ⅰ）当点M变化时，求动点P的轨迹G的方程；
（Ⅱ）过点F2且不与x轴重合的直线L与曲线G相交于A，B两点，过点B作x轴的平行线与直线x=2相交于点C，则直线AC是否恒过定点，若是请求出该定点，若不是请说明理由．

【题目】在平面直角坐标系中，直线l的参数方程为 （t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12． （Ⅰ）写出直线l的极坐标方程与曲线C的直角坐标方程；
（Ⅱ）已知与直线l平行的直线l'过点M（1，0），且与曲线C交于A，B两点，试求|AB|．

【题目】将函数 的图象向左平移 个单位长度后，所得函数g（x）的图象关于原点对称，则函数f（x）在 的最大值为（ ）
A.0
B.
C.
D.1

【题目】已知函数f（x）=（a+1）lnx﹣x2 ， ．
（1）讨论函数f（x）的单调区间；
（2）若函数f（x）与g（x）在（0，+∞）上的单调性正好相反． （Ⅰ）对于 ，不等式 恒成立，求实数t的取值范围；
（Ⅱ）令h（x）=xg（x）﹣f（x），两正实数x1、x2满足h（x1）+h（x2）+6x1x2=6，证明0＜x1+x2≤1．

【题目】已知数列{an}，an=（2n+m）+（﹣1）n（3n﹣2）（m∈N* ， m与n无关），若 a2i﹣1≤k2﹣2k﹣1对一切m∈N*恒成立，则实数k的取值范围为 ．

【题目】若f（x）为奇函数，且x0是y=f（x）﹣ex的一个零点，则下列函数中，﹣x0一定是其零点的函数是（ ）
A.y=f（﹣x）e﹣x﹣1
B.y=f（x）ex+1
C.y=f（x）ex﹣1
D.y=f（﹣x）ex+1

【题目】已知P是椭圆 上任意一点，过椭圆的右顶点A和上顶点B分别作x轴和y轴的垂线，两垂线交于点C，过P作AC，BC的平行线交BC于点M，交AC于点N，交AB于点D，E，矩形PMCN的面积是S1 ， 三角形PDE的面积是S2 ， 则 =（ ）
A.2
B.1
C.
D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网