题目内容
1．已知函数y=f（x）是定义在R上的偶函数，在（-∞，0]上单调递减，且有f（3）=0，则使得$f（{log_{\frac{1}{3}}}x）＜0$的x的范围为（ ）| A． | （-3，3） | B． | （-∞，-3）∪（3，+∞） | C． | $（-∞，\frac{1}{27}）∪（27，+∞）$ | D． | $（\frac{1}{27}，27）$ |
分析 由f（x）为偶函数，f（x）在（-∞，0）上的单调性，可判断f（x）在（0，+∞）上的单调性，由f（3）=0，可得f（-3）=0，从而据题意可作出f（x）的草图，由图象即可解得不等式．
解答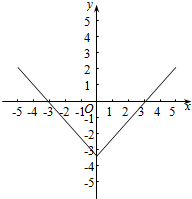 
解：因为f（x）在（-∞，0）上单调递减，又f（x）为R上的偶函数，
所以f（x）在（0，+∞）上单调递增，
由f（3）=0可得f（-3）=0，
作出满足题意的函数f（x）的草图，如图：
由图象可得，-3＜$lo{g}_{\frac{1}{3}}x$＜3．
∴$\frac{1}{27}＜x＜27$
故选D．
点评 本题考查函数的奇偶性、单调性及其应用，数形结合解决本题简洁直观，注意体会．
练习册系列答案
相关题目
9．函数y=sin（-2x+$\frac{π}{6}$）的单调递增区间是（ ）
| A． | [-$\frac{π}{6}$+2kπ，$\frac{π}{3}$+2kπ]（k∈Z） | B． | $[\frac{π}{3}+2kπ，\frac{5π}{6}+2kπ]（k∈Z）$ | ||
| C． | [-$\frac{π}{6}$+kπ，$\frac{π}{3}$+kπ]（k∈Z） | D． | $[\frac{π}{3}+kπ，\frac{5π}{6}+kπ]（k∈Z）$ |