题目内容
6．角α始边与x轴非负半轴重合，终边经过点P（-2，1），则tanα=-$\frac{1}{2}$．分析 直接利用正切函数的定义，即可得出结论．
解答 解：∵角α始边与x轴非负半轴重合，终边经过点P（-2，1），
∴tanα=-$\frac{1}{2}$．
故答案为：-$\frac{1}{2}$．
点评 本题考查任意角的三角函数的定义，掌握三角函数的定义是解题的关键，属于基础题．
练习册系列答案
相关题目
如图，在平行四边形ABCD中，∠BAD=120°，AB=2，AD=1，若$\overrightarrow{DE}=t\overrightarrow{DC}$，AE⊥BD，则实数t的值为$\frac{2}{5}$．
1．已知函数y=f（x）是定义在R上的偶函数，在（-∞，0]上单调递减，且有f（3）=0，则使得$f（{log_{\frac{1}{3}}}x）＜0$的x的范围为（ ）
| A． | （-3，3） | B． | （-∞，-3）∪（3，+∞） | C． | $（-∞，\frac{1}{27}）∪（27，+∞）$ | D． | $（\frac{1}{27}，27）$ |
11．
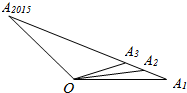如图，O为直线A1A2015外一点，若A1，A2，A3，A4，A5…A2015中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（ ）
如图，O为直线A1A2015外一点，若A1，A2，A3，A4，A5…A2015中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（ ）| A． | 2014（$\overrightarrow{a}+\overrightarrow{b}$） | B． | 2015（$\overrightarrow{a}+\overrightarrow{b}$） | C． | $\frac{2014}{2}$（$\overrightarrow{a}+\overrightarrow{b}$） | D． | $\frac{2015}{2}$（$\overrightarrow{a}+\overrightarrow{b}$） |