题目内容
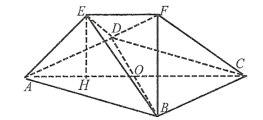
【题目】在如图所示的几何体
中，平面
平面
，四边形
和四边形都是正方形，且边长为
，
是
的中点.
（1）求证：直线
平面
；
（2）求二面角
的大小.
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）连结
交
于
，根据平行四边形性质得是中点，再根据三角形中位线性质得
，最后根据线面平行判定定理得结论,（2）根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求夹角,最后根据二面角与向量夹角相等或互补关系求二面角.
试题解析：（1）∵且
，
与
交于点
，
与
交于点
∴平面
平面
，∴几何体
是三棱柱
又平面
平面
，
，∴
平面，故几何体是直三棱柱
（1）四边形
和四边形都是正方形，所以
且
，所以四边形
为矩形；于是，连结交于，连结
，是中点，又
是的中点，故是三角形D
的中位线，，注意到在平面
外，在平面内，∴直线
平面
（2）由于平面 
平面，，∴
平面，所以
.于是
，，两两垂直.以
，，所在直线分别为
，
，
轴建立空间直角坐标系，因正方形边长为
，且为中点，所以
，
，
，
于是
，
，设平面
的法向量为
则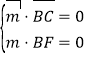
，解之得
，同理可得平面
的法向量
，∴
记二面角
的大小为
，依题意知，为锐角，
，
即求二面角的大小为
快捷英语周周练系列答案
【题目】交管部门为宣传新交规举办交通知识问答活动，随机对该市
岁的人群抽样了
人，回答问题统计结果如图表所示：
分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
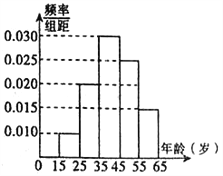
（1）分别求出
，
，
，
的值；
（2）从第
，
，
组回答正确的人中用分层抽样方法抽取
人，则第，，组每组应各抽取多少人？
（3）在（2）的前提下，决定在所抽取的人中随机抽取人颁发幸运奖，求：所抽取的人中至少有一个第组的人的概率.
【题目】某二手车交易市场对某型号二手汽车的使用年数
与销售价格
（单位：万元/辆）进行整理，得到如下的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
（1）试求关于
的回归直线方程；（参考公式：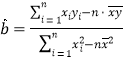
，
.）
（2）已知每辆该型号汽车的收购价格为
万元，根据（1）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润
最大？
