题目内容
已知f(x)=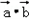 ,其中向量
,其中向量 =
=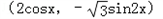 ,
,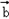 =(cosx,1)(x∈R)
=(cosx,1)(x∈R)
(Ⅰ)求f (x)的周期和单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a,b,c,f(A)=﹣1,a=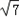 ,
,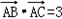 ,求边长b和c的值(b>c).
,求边长b和c的值(b>c).
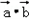 ,其中向量
,其中向量 =
=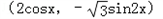 ,
,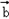 =(cosx,1)(x∈R)
=(cosx,1)(x∈R)(Ⅰ)求f (x)的周期和单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a,b,c,f(A)=﹣1,a=
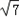 ,
,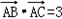 ,求边长b和c的值(b>c).
,求边长b和c的值(b>c).解:(Ⅰ)由题意知:
f(x)=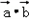 =
=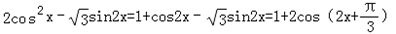 ,
,
∴f(x)的最小正周期 T=π
由 2kπ≤2x+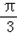 ≤2kπ+π,k∈z,
≤2kπ+π,k∈z,
求得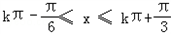 ,k∈z.
,k∈z.
∴f(x)的单调递减区间[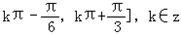 ,k∈z.
,k∈z.
(2)∵f (A)=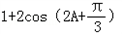 =﹣1,
=﹣1,
∴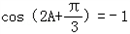 ,
,
又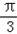 <2A+
<2A+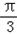 <
<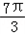 ,
,
∴2A+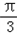 =π,A=
=π,A=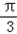 .
.
∵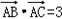 即bc=6,
即bc=6,
由余弦定理得 a2=b2+c2﹣2bccosA=(b+c)2﹣3bc,
7=(b+c)2﹣18,b+c=5,
又b>c,
∴b=3,c=2
f(x)=
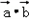 =
=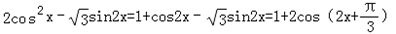 ,
,∴f(x)的最小正周期 T=π
由 2kπ≤2x+
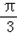 ≤2kπ+π,k∈z,
≤2kπ+π,k∈z,求得
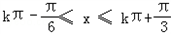 ,k∈z.
,k∈z.∴f(x)的单调递减区间[
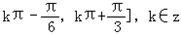 ,k∈z.
,k∈z.(2)∵f (A)=
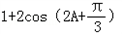 =﹣1,
=﹣1,∴
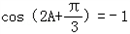 ,
,又
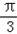 <2A+
<2A+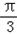 <
<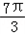 ,
,∴2A+
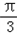 =π,A=
=π,A=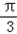 .
.∵
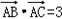 即bc=6,
即bc=6,由余弦定理得 a2=b2+c2﹣2bccosA=(b+c)2﹣3bc,
7=(b+c)2﹣18,b+c=5,
又b>c,
∴b=3,c=2

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目







