题目内容
已知f(x)=|logax|,其中0<a<1,则f(2),f(
),f(
)由大到小排列为
| 1 |
| 3 |
| 1 |
| 4 |
f(
),f(
),f(2)
| 1 |
| 4 |
| 1 |
| 3 |
f(
),f(
),f(2)
.| 1 |
| 4 |
| 1 |
| 3 |
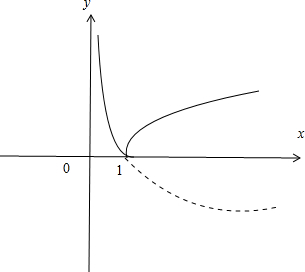
分析:作出函数f(x)=|logax|的函数的图象,由于f(2)=f(
)结合函数f(x)=|logax|在(0,1)上单调性可判断
| 1 |
| 2 |
解答:解:作出函数f(x)=|logax|的函数的图象如图所示
∵f(2)=|loga2|=|loga
|=f(
)
又由于
<
<
且函数f(x)=|logax|在(0,1)上单调递减
∴f(
)>f(
)>f(
)即f(
)>f(
)>f(2)
故答案为:f(
),f(
),f(2)
∵f(2)=|loga2|=|loga
| 1 |
| 2 |
| 1 |
| 2 |
又由于
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
∴f(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
故答案为:f(
| 1 |
| 4 |
| 1 |
| 3 |

点评:本题主要考查了利用对数函数的单调性比较对数值的大小,解答本题的关键是要根据对数函数的图象及函数的图象变换准确作出函数f(x)的图象,体现了数形结合思想的应用

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
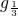 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.