题目内容
函数
的导数为
，则（ ）
A． | B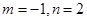． | C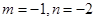． | D． |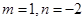
D
解析试题分析：因为，所以
，所以
，且
，解得.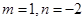
考点：本小题主要考查导数的运算，考查求导公式的应用.
点评：熟记基本初等函数的导数公式及四则运算法则是正确求导的基础.
练习册系列答案
相关题目
对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有（ ）
| A．f（0）＋f（2）<2f（1） | B．f（0）＋f（2）£2f（1） |
| C．f（0）＋f（2）³2f（1） | D．f（0）＋f（2）>2f（1） |
已知
,则（ ）
A． | B． | C． | D．以上都有可能 |
函数
图象如图，则函数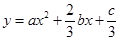
的单调递增区间为（ ）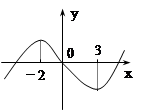
A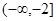． | B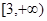． | C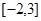． | D． |
已知函数
有两个零点
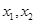，则（ ）
A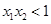． | B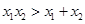． | C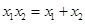． | D． |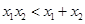
函数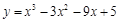
在区间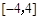
上的最大值为( ）.
| A．10 | B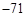． | C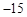． | D． |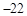
设点
在曲线
上，点
在曲线
上，则
最小值为 （ ）
A． | B． | C． | D． |
若曲线
在点
处的切线平行于直线
，则点的坐标为
| A．（1，3） | B．（－1，3） | C．（1，0） | D．（－1，0） |
若函数
的导函数
,则函数
的单调递减区间是 ( )
A． | B． | C． | D． |