题目内容
设点 在曲线
在曲线 上,点
上,点 在曲线
在曲线 上,则
上,则 最小值为 ( )
最小值为 ( )
A. | B. | C. | D. |
B
解析试题分析:利用互为反函数的两个函数图象的性质结合导数的有关知识求解
如图所示,由题意知函数 与
与 互为反函数,它们的图象关于直线
互为反函数,它们的图象关于直线 对称,两曲线上点之间的最小距离就是
对称,两曲线上点之间的最小距离就是 与
与 上点的最小距离的
上点的最小距离的 倍,设
倍,设 上点
上点 处切线与
处切线与 平行,有
平行,有 与
与 上点的最小距离是
上点的最小距离是 ,所以所求距离为
,所以所求距离为
考点:本小题主要考查了互为反函数的两个函数的图象之间的关系及其应用,过曲线上一点的切线的求法及点点到直线的距离公式的应用,也考查了数形结合的思想。
点评:解决此题的关键是发现两个函数是互为反函数的,掌握互为反函数的两个函数的图象之间的关系,并能够通过图象发现 何时最短,本题难度较大。
何时最短,本题难度较大。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知二次函数 的图象如图所示,则它与
的图象如图所示,则它与 轴所围图形的面积为:
轴所围图形的面积为:
A. | B. | C. | D. |
直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
A.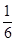 | B.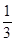 | C.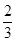 | D. |
函数 的导数为
的导数为 ,则( )
,则( )
A. | B.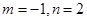 | C.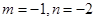 | D.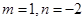 |
函数 的单调递增区间是 ( )
的单调递增区间是 ( )
A. | B.(0,3) | C.(1,4) | D.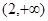 |
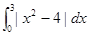 = ( )
= ( )
A. | B.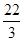 | C.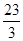 | D. |
曲线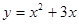 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是
| A.4 | B.5 | C.6 | D.7 |
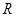 上的函数
上的函数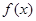 满足
满足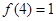 ,
,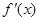 为
为 的图象如图所示.若两正数
的图象如图所示.若两正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )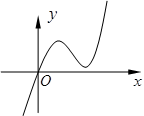

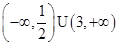

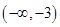
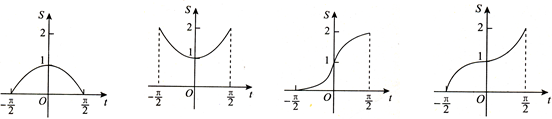
 的图象上有一点
的图象上有一点 ,此函数图象与
,此函数图象与 轴及直线
轴及直线 围成图形(如图阴影部分)的面积为
围成图形(如图阴影部分)的面积为 ,则
,则 的函数关系
的函数关系 的图象可以是( )
的图象可以是( )