题目内容
函数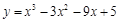
在区间
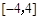上的最大值为( ）.
| A．10 | B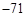． | C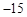． | D． |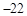
A
解析试题分析：因为
,由
,
得
，因为f(x)的极大值为f(-1)=10,而f(4)=-15.所以f(x)的最大值为10.
考点：导数求连续函数在闭区间上的最值.
点评：连续函数在闭区间上的最值不在区间端点处取得，就在极点处取得，所以通过比较端点函数值与极值比较即可确定最值.
练习册系列答案
阅读快车系列答案
相关题目
是
的导函数，
若函数
的导函数
，则使得函数
单调递减的一个充分不必要条件是
（ ）
| A．（0，1） | B．[0，2] | C．（2，3） | D．（2，4） |
曲线
在点（－1，－3）处的切线方程是
A． | B． | C． | D． |
函数
的导数为
，则（ ）
A． | B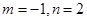． | C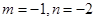． | D． |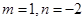
函数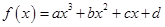
的图象（如图），则函数
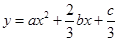的单调递增区间是（ ）
A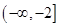． | B． |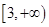
C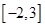． | D． |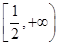
= （ ）
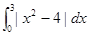A． | B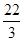． | C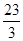． | D． |
函数
的导函数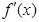
的图象大致是( )
A． | B． |
C． | D． |
若函数
（
）有大于零的极值点，则实数
范围是 （ ）
A． | B． | C． | D． |