题目内容
4.已知数列{an}满足a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N+),则a1+a2+a3+…+a2015的值为$-\frac{1765}{3}$.分析 由已知求出数列前几项,可以发现数列是以4为周期的周期数列,由此求得a1+a2+a3+…+a2015的值.
解答 解:由a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,得${a}_{2}=\frac{1+{a}_{1}}{1-{a}_{1}}=\frac{1+2}{1-2}=-3$,
${a}_{3}=\frac{1-3}{1+3}=-\frac{1}{2}$,${a}_{4}=\frac{1-\frac{1}{2}}{1+\frac{1}{2}}=\frac{1}{3}$,${a}_{5}=\frac{1+\frac{1}{3}}{1-\frac{1}{3}}=2$,
由上可知,数列{an}是以4为周期的周期数列,
且${a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}=2-3-\frac{1}{2}+\frac{1}{3}$=$-\frac{7}{6}$,
∴a1+a2+a3+…+a2015=503×$(-\frac{7}{6})$+2-3-$\frac{1}{2}$=$-\frac{1765}{3}$.
故答案为:$-\frac{1765}{3}$.
点评 本题考查了数列递推式,关键是对数列周期性的发现,是中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
19.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)一个周期内的一系列对应值如表:
(1)求f(x)的解析式;
(2)求函数g(x)=f(x)+$\sqrt{3}$sin2x的单调递增区间.
| x | 0 | $\frac{π}{6}$ | $\frac{π}{4}$ | $\frac{π}{2}$ |
| y | 1 | $\frac{1}{2}$ | 0 | -1 |
(2)求函数g(x)=f(x)+$\sqrt{3}$sin2x的单调递增区间.
13.设复数z1=l+2i,z2=l-ai,若z1•z2为实数,则实数a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交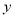 轴于
轴于 ,且
,且 ,
, 为坐标原点.
为坐标原点. 的方程;
的方程;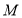 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点. 如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点.求证:AP•BC=AC•CP.
如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点.求证:AP•BC=AC•CP. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M是AC的中点,∠CAD=30°,AB=2,点N在线段PB上,且$\frac{PN}{NB}=\frac{1}{3}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M是AC的中点,∠CAD=30°,AB=2,点N在线段PB上,且$\frac{PN}{NB}=\frac{1}{3}$.