题目内容
13.设数列{an}的n项和为Sn,且a1=a2=1,{nSn+(n+2)an}为等差数列,则{an}的通项公式an=$\frac{n}{{2}^{n-1}}$.分析 令bn=nSn+(n+2)an,由已知得b1=4,b2=8,从而bn=nSn+(n+2)an=4n,进一步得到{$\frac{{a}_{n}}{n}$}是以$\frac{1}{2}$为公比,1为首项的等比数列,由此能求出{an}的通项公式.
解答 解:设bn=nSn+(n+2)an,
∵数列{an}的前n项和为Sn,且a1=a2=1,
∴b1=4,b2=8,
∴bn=b1+(n-1)×(8-4)=4n,
即bn=nSn+(n+2)an=4n
当n≥2时,Sn-Sn-1+(1+$\frac{2}{n}$)an-(1+$\frac{2}{n-1}$)an-1=0
∴$\frac{2(n+1)}{n}{a}_{n}$=$\frac{n+1}{n-1}{a}_{n-1}$,
即2•$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$,
∴{$\frac{{a}_{n}}{n}$}是以$\frac{1}{2}$为公比,1为首项的等比数列,
∴$\frac{{a}_{n}}{n}$=$(\frac{1}{2})^{n-1}$,
∴${a}_{n}=\frac{n}{{2}^{n-1}}$.
点评 本题考查数列的通项公式的求法,考查等差数列的性质,解答的关键是注意构造法和等差数列、等比数列的性质的合理运用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=-ln(1-x),函数f(x)=$\left\{\begin{array}{l}{{x}^{3},x≤0}\\{g(x),x>0}\end{array}\right.$,若f(2-x2)>f(x),则x的取值范围是( )
| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,1)∪(2,+∞) | C. | (-2,1) | D. | (1,2) |
 的棱长为
的棱长为 ,半径为
,半径为 的圆
的圆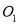 在平面
在平面 内,其圆心
内,其圆心 为圆
为圆 的外接球的表面积为( )
的外接球的表面积为( ) B.
B. C.
C.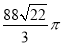 D.
D.
 如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于7.
如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于7.