题目内容
已知: 证明:
证明: .
.
 证明:
证明: .
.分析法或综合法
试题分析:证法一(用分析法):
 , (2分)
, (2分)要证
 ,(4分)
,(4分)只须证:
 ,(6分)
,(6分)即只须证:
 ,(8分)
,(8分) ,
, 成立,即
成立,即 成立,
成立,∴原不等式成立。(10分)
证法二(用综合法):∵
 (4分)
(4分)∵
 ,
, ,∴
,∴ ,(6分)
,(6分)∴
 ,
, (8分)
(8分)∴
 ,
,∴
 ,原不等式成立。(10分)
,原不等式成立。(10分)点评:中档题,不等式的证明方法,通常考虑“差比法”“分析法”“综合法”“反证法”“放缩法”“换元法”“数学归纳法”等。当题目的条件较少时,利用“分析法”往往通过“执果索因”,可以探求得到,证明的途径。

练习册系列答案
相关题目
 ,
, ,
, 成等差数列.(1)比较
成等差数列.(1)比较 与
与 的大小,并证明你的结论;(2)求证B不可能是钝角
的大小,并证明你的结论;(2)求证B不可能是钝角 满足
满足 ,求证
,求证 ≥
≥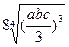
 时,等号成立
时,等号成立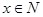 满足
满足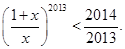 数列
数列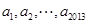 是公差为
是公差为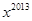 ,首项
,首项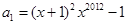 的等差数列; 数列
的等差数列; 数列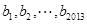 是公比为
是公比为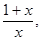 首项
首项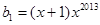 的等比数列,求证:
的等比数列,求证: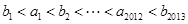 。
。 ,求证:
,求证:
 .
.