题目内容
设a=(sinx-1,cosx-1),b=(
| ||
| 2 |
| ||
| 2 |
(1)若a为单位向量,求x的值;
(2)设f(x)=a•b,则函数y=f(x)的图象是由y=sinx的图象按c平移而得,求c.
分析:(1)根据向量模的运算和单位向量模为1可得(sinx-1)2+(cosx-1)2=1,进而得到答案.
(2)根据向量数量积的运算将函数f(x)表示出,即f(x)=sin(x+
)-
,再根据三角函数的平移变换可得答案.
(2)根据向量数量积的运算将函数f(x)表示出,即f(x)=sin(x+
| π |
| 4 |
| 2 |
解答:解:(1)∵|a|=1,∴(sinx-1)2+(cosx-1)2=1,
即sinx+cosx=1,
sin(x+
)=1,
sin(x+
)=
,
∴x=2kπ或x=2kπ+
,k∈Z.
(2)∵a•b=sin(x+
)-
.
∴f(x)=sin(x+
)-
,
由题意得c=(-
,-
).
即sinx+cosx=1,
| 2 |
| π |
| 4 |
sin(x+
| π |
| 4 |
| ||
| 2 |
∴x=2kπ或x=2kπ+
| π |
| 2 |
(2)∵a•b=sin(x+
| π |
| 4 |
| 2 |
∴f(x)=sin(x+
| π |
| 4 |
| 2 |
由题意得c=(-
| π |
| 4 |
| 2 |
点评:本题主要考查向量数量积的运算和向量模的求法.属基础题.一定要记住向量数量积的运算法则.

练习册系列答案
相关题目
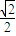 ,
,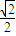 ).
).