题目内容
《莱因德纸草书》( Rhind Papyrus )是世界上最古老的数学著作之一. 书中有一道这样的题目:把100个面包分给5个人,使每个所得成等差数列,且使最大的三份之和的| 1 | 7 |
分析:由每一个人分得的面包成等差数列设出各项,分别根据等差数列的前5项之和等于100,最大的三份之和的
是较小的两份之和列出两个方程,联立即可求出最小1份的量.
| 1 |
| 7 |
解答:解:设每个人由少到多的顺序得到面包分别为a1,a2,a3,a4,a5,
因为每个所得的面包成等差数列设公差为d,则有100=5a1+10d①;
又最大的三份之和的
是较小的两份之和得到:较小的两份之和a1+a2=2a1+d=
×100②.
联立①②解得a1=
.
故答案为
因为每个所得的面包成等差数列设公差为d,则有100=5a1+10d①;
又最大的三份之和的
| 1 |
| 7 |
| 1 |
| 8 |
联立①②解得a1=
| 5 |
| 3 |
故答案为
| 5 |
| 3 |
点评:本题为一道中档题,要求学生灵活运用等差数列的通项公式及前n项和的公式进行化简求值.此题的突破点在于设出等差数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是较小的两份之和,问最小1份为( )
是较小的两份之和,问最小1份为( ) B.
B.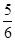 C.
C.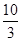 D.
D.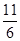
 是较少两份面包数之和,问最少的1份面包数为
是较少两份面包数之和,问最少的1份面包数为