题目内容
【题目】已知二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,
,![]() ,设
,设![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )
)![]() 如何取值时,函数
如何取值时,函数![]() 存在极值点,并求出极值点.
存在极值点,并求出极值点.
(![]() )若
)若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析:(1)根据二次不等式解集与二次方程根的关系可得![]() ,解得
,解得![]() 的值.(2)先求导数,再研究导函数零点:没有零点就没有极值点,有零点但不在定义区间,也不是零点;零点在定义区间且附近导函数变号才是零点;(3)先根据二项展开式化简不等式左边式子,并根据基本不等式放缩,再根据倒序相加法求中间的和,利用基本不等式放缩即得结论.
的值.(2)先求导数,再研究导函数零点:没有零点就没有极值点,有零点但不在定义区间,也不是零点;零点在定义区间且附近导函数变号才是零点;(3)先根据二项展开式化简不等式左边式子,并根据基本不等式放缩,再根据倒序相加法求中间的和,利用基本不等式放缩即得结论.
试题解析:(![]() )因为关于
)因为关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,
,
即不等式![]() 的解集为
的解集为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
(![]() )由(
)由(![]() )得
)得![]() ,
,
所以![]() 的定义域为
的定义域为![]() ,
,
所以![]() ,
,
方程![]() (*)的判别式
(*)的判别式
![]() .
.
①当![]() 时,
时,![]() ,方程(*)的两个实根为
,方程(*)的两个实根为![]() ,
,![]() ,
,
则![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 有极小值点
有极小值点![]() .
.
②当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() ,若
,若![]() ,
,
则![]() ,
,![]() ,故
,故![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增.所以函数
上单调递增.所以函数![]() 没有极值点,
没有极值点,
若![]() 时,
时,![]() ,
,![]() ,
,
则![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 有极小值点
有极小值点![]() ,有极大值点
,有极大值点![]() ,
,
综上所述,当![]() 时,
时,![]() 取任意实数,函数
取任意实数,函数![]() 有极小值点
有极小值点![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 有极小值点
有极小值点![]() ,有极大值点
,有极大值点![]() ,
,
(其中![]() ,
,![]() ).
).
(![]() )因为
)因为![]() ,所以
,所以![]() ,
,
所以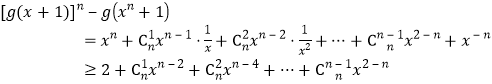 ,
,
令![]() ,
,
则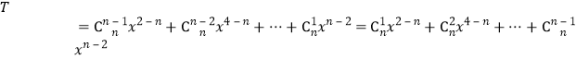 ,
,
因为![]() ,所以
,所以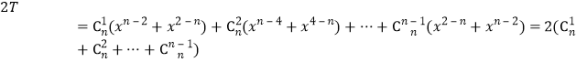
![]() ,
,
所以![]() ,即
,即![]() .
.

练习册系列答案
相关题目