题目内容
设数列{an}的首项a1=1,前n项和为Sn,且Sn+1=2n2+3n+1,n∈N*。
(1)求数列{an}的通项公式an;
(2)设数列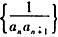 的前n项和为Tn,是否存在最大正整数β,使得对[1,β+1)内的任意n∈N*,不等式Tn<
的前n项和为Tn,是否存在最大正整数β,使得对[1,β+1)内的任意n∈N*,不等式Tn<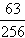 恒成立?若存在,求出β的值;若不存在,请说明理由。
恒成立?若存在,求出β的值;若不存在,请说明理由。
(1)求数列{an}的通项公式an;
(2)设数列
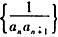 的前n项和为Tn,是否存在最大正整数β,使得对[1,β+1)内的任意n∈N*,不等式Tn<
的前n项和为Tn,是否存在最大正整数β,使得对[1,β+1)内的任意n∈N*,不等式Tn<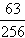 恒成立?若存在,求出β的值;若不存在,请说明理由。
恒成立?若存在,求出β的值;若不存在,请说明理由。解:(1)由
得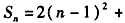
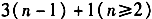
∴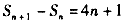
∴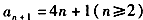
∴
当n=1时,S2=6
∵a1=1
∴a2=5
∵a1=1,a2=5同样适用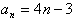
∴数列{an}的通项公式 。
。
(2)∵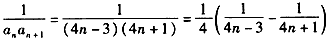
∴
∵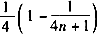 在
在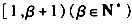 内单调递增
内单调递增
∴
∴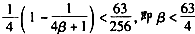
∵β∈N*,
∴β≤15
∴存在满足条件的最大正整数β=15,使不等式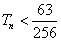 恒成立。
恒成立。

得
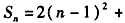
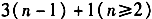
∴
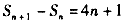
∴
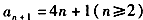
∴

当n=1时,S2=6
∵a1=1
∴a2=5
∵a1=1,a2=5同样适用
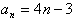
∴数列{an}的通项公式
 。
。(2)∵
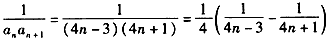
∴

∵
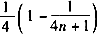 在
在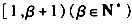 内单调递增
内单调递增∴

∴
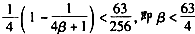
∵β∈N*,
∴β≤15
∴存在满足条件的最大正整数β=15,使不等式
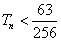 恒成立。
恒成立。
练习册系列答案
相关题目
