题目内容
四面体ABCD中，AB=CD=6，其余的棱长均为5，则与该四面体各个表面都相切的内切球的半径长等于________．
分析：把四面体分割成四个小三棱锥，根据体积相等，即可得解
解答：
解：取CD的中点E连接AE、BE，取AB的中点F，连接EF由题意知AE⊥CD，BE⊥CD
又∵AE∩BE=E
∴CD⊥面ABE
又AB=CD=6，其余的棱长均为5
∴AD=5，DE=3
∴AE=4，同理BE=4
∴等腰△ABE底边AB上的高为EF=
∴△ABE的面积S=
∴三棱锥ABCD的体积V=
=
又
设内切球的半径为R，则球心O到每个表面的距离为R，且球心O到每个表面的距离为R
∴三棱锥ABCD的体积V=
=
∴
故答案为：
点评：本题考查求几何体的体积，利用等体积法求半径，本题采取了割补法的技巧．属中档题
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
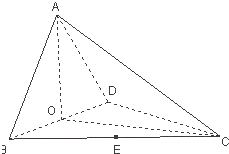如图，四面体ABCD中，O、E分别是BD、BC的中点，CA=CB=CD=BD=2，AB=AD=
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
=a, 
=b, 
=c,G为△BCD的重心，则
=__________.
= a，
= b，
= c，G∈平面ABC．则G为△ABC的重心的充分必要条件是
(a+b+c)；