题目内容
已知函数
(Ⅰ)如果f(x)在区间(1,2)不单调,求a的取值范围;
(Ⅱ)如果a>0,设函数g(x)=f(x)+ax,求函数g(x)的极大值.
解:(I
设h(x)=ax2-x-a=0的两个根为x1,x2
由韦达定理得x1•x2=1
∵f(x)在区间(1,2)不单调
∴h(x)=0在区间(1,2)上h(x)=0有且仅有一个根,另一个根小于1,
则h(1)h(2)<0
即(a-1-a)(4a-2-a)<0
解得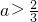
(II)
①当a=1时,函数g(x)无极值
②当a>1时,在 ,g′(x)>0,g(x)单调递增,
,g′(x)>0,g(x)单调递增,
在 上,g′(x)<0,g(x)单调递减
上,g′(x)<0,g(x)单调递减
在(0,+∞)时,g′(x)>0,g(x)单调递增
∴当 时,g(x)取得极大值为
时,g(x)取得极大值为
③当0<a<1时,函数g(x)在区间 上是增函数,在区间
上是增函数,在区间 是减函数
是减函数
所以函数g(x)的极大值为g(0)=0
分析:(I)求出函数的导函数,将导函数的分子看成一个函数h(x),将f(x)在区间(1,2)不单调转化为方程h(x)=0的根的分布问题,结合二次函数的图象写出限制条件求出a的范围.
(II)求出g(x)的导函数,通过对导函数的两个根大小的讨论判断出导函数的符号,进一步判断出函数的单调性,根据极值的定义求出函数g(x)的极大值.
点评:解决函数在某区间不单调问题常转化为在区间函数有极值;求函数的极值问题,一般求出导函数,令导函数为0,判断根左右两边的导函数符号,求出极值,若含参数时,一般要讨论.

设h(x)=ax2-x-a=0的两个根为x1,x2
由韦达定理得x1•x2=1
∵f(x)在区间(1,2)不单调
∴h(x)=0在区间(1,2)上h(x)=0有且仅有一个根,另一个根小于1,
则h(1)h(2)<0
即(a-1-a)(4a-2-a)<0
解得
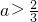
(II)

①当a=1时,函数g(x)无极值
②当a>1时,在
 ,g′(x)>0,g(x)单调递增,
,g′(x)>0,g(x)单调递增,在
 上,g′(x)<0,g(x)单调递减
上,g′(x)<0,g(x)单调递减在(0,+∞)时,g′(x)>0,g(x)单调递增
∴当
 时,g(x)取得极大值为
时,g(x)取得极大值为
③当0<a<1时,函数g(x)在区间
 上是增函数,在区间
上是增函数,在区间 是减函数
是减函数所以函数g(x)的极大值为g(0)=0
分析:(I)求出函数的导函数,将导函数的分子看成一个函数h(x),将f(x)在区间(1,2)不单调转化为方程h(x)=0的根的分布问题,结合二次函数的图象写出限制条件求出a的范围.
(II)求出g(x)的导函数,通过对导函数的两个根大小的讨论判断出导函数的符号,进一步判断出函数的单调性,根据极值的定义求出函数g(x)的极大值.
点评:解决函数在某区间不单调问题常转化为在区间函数有极值;求函数的极值问题,一般求出导函数,令导函数为0,判断根左右两边的导函数符号,求出极值,若含参数时,一般要讨论.

练习册系列答案
相关题目
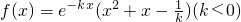 .
.
 .
. .
.
 ,求锐角α.
,求锐角α.