题目内容
已知圆C的圆心在直线l:3x-y=0上,且与直线l1:x-y+4=0相切.
(1)若直线x-y=0截圆C所得弦长为2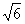 ,求圆C的方程.
,求圆C的方程.
(2)若圆C与圆x2+y2-4x-12y+8=0外切,试求圆C的半径.
(3)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
设圆C的圆心坐标为(a,3a),则它的半径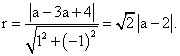
(1)圆心C到直线x-y=0的距离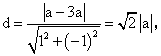
因而该直线截圆C所得弦长为
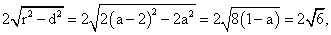
所以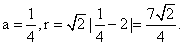
圆C的方程为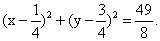
(2)两圆的连心线长为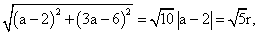 因为两圆外切,
因为两圆外切,
所以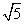 r=r+4
r=r+4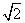 ,所以r=
,所以r=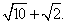
(3)如果存在另一条公切线,则它必过l与l1的交点(2,6).
①若斜率不存在,则其方程为x=2,圆心C到它的距离|a-2|=r=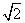 |a-2|,由于方程需要对任意的a都成立,因此无解,所以它不是公切线.
|a-2|,由于方程需要对任意的a都成立,因此无解,所以它不是公切线.
②若斜率存在,设公切线的方程为y-6=k(x-2),
即kx-y+6-2k=0,
所以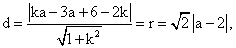
所以k2+6k-7=0,解出k=1或k=-7.
k=1时直线与l1重合,k=-7时,
直线方程为7x+y-20=0.
所以还存在一条公切线,其方程为7x+y-20=0.

练习册系列答案
相关题目
 .
. ,与正方体各棱都相切的球的半径为
,与正方体各棱都相切的球的半径为 ,正方体的外接球的半径为
,正方体的外接球的半径为 ,则
,则 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.1 C. 3 D0
B.1 C. 3 D0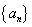 的前
的前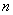 项和为
项和为 ,那么
,那么
 中,
中, ,那么
,那么 .
.