题目内容
如图所示,多面体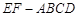 中,
中, 是梯形,
是梯形,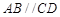 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
, ,
,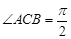 .
.

(1)求证: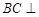 平面
平面 ;
;
(2)若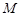 是棱
是棱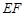 上一点,
上一点,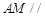 平面
平面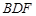 ,求
,求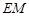 ;
;
(3)求二面角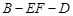 的平面角的余弦值.
的平面角的余弦值.
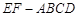 中,
中, 是梯形,
是梯形,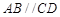 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
, ,
,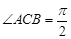 .
.
(1)求证:
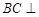 平面
平面 ;
;(2)若
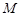 是棱
是棱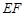 上一点,
上一点,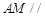 平面
平面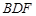 ,求
,求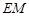 ;
;(3)求二面角
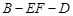 的平面角的余弦值.
的平面角的余弦值.(1)见解析 (2) . (3)
. (3) .
.
 . (3)
. (3) .
.(1)易证: ,再根据平面ACFE
,再根据平面ACFE 平面ABCD,利用面面垂直的性质定理转化为
平面ABCD,利用面面垂直的性质定理转化为 .
.
(2)连接BD,交AC于O点,若 则
则 .从而再根据O的位置确定M的位置求出EM的长度.
.从而再根据O的位置确定M的位置求出EM的长度.
(3)以C为原点,CA、CB、CF分别为x轴,y轴,z轴建立空间直角坐标系C-xyz,然后分别求出平面BEF和平面EFD的法向量,利用向量法求二面角B-EF-D的平面角的余弦值
(1)平面 ,
,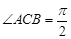 ,从而
,从而 .又因为
.又因为 面
面 ,平面
,平面 平面
平面 ,所以
,所以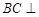 平面
平面 .
.
(2)连接 ,记
,记 ,在梯形
,在梯形 中,因为
中,因为 ,
,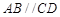 ,所以
,所以 ,
, ,
, ,从而
,从而 .又因为
.又因为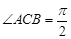 ,
, ,所以
,所以 .连接
.连接 ,由
,由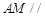 平面
平面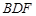 得
得 ,因为
,因为 是矩形,所以
是矩形,所以 .
.
(3)以 为原点,
为原点, 、
、 、
、 分别为
分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系
轴建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则有
,则有 ,即
,即 ,解得
,解得 .
.
同理可得平面 的一个法向量为
的一个法向量为 ,观察知二面角
,观察知二面角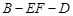 的平面角为锐角,所以其余弦值为
的平面角为锐角,所以其余弦值为 .
.
 ,再根据平面ACFE
,再根据平面ACFE 平面ABCD,利用面面垂直的性质定理转化为
平面ABCD,利用面面垂直的性质定理转化为 .
.(2)连接BD,交AC于O点,若
 则
则 .从而再根据O的位置确定M的位置求出EM的长度.
.从而再根据O的位置确定M的位置求出EM的长度.(3)以C为原点,CA、CB、CF分别为x轴,y轴,z轴建立空间直角坐标系C-xyz,然后分别求出平面BEF和平面EFD的法向量,利用向量法求二面角B-EF-D的平面角的余弦值
(1)平面
 ,
,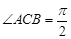 ,从而
,从而 .又因为
.又因为 面
面 ,平面
,平面 平面
平面 ,所以
,所以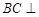 平面
平面 .
.(2)连接
 ,记
,记 ,在梯形
,在梯形 中,因为
中,因为 ,
,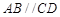 ,所以
,所以 ,
, ,
, ,从而
,从而 .又因为
.又因为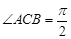 ,
, ,所以
,所以 .连接
.连接 ,由
,由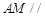 平面
平面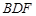 得
得 ,因为
,因为 是矩形,所以
是矩形,所以 .
.(3)以
 为原点,
为原点, 、
、 、
、 分别为
分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系
轴建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则有
,则有 ,即
,即 ,解得
,解得 .
.同理可得平面
 的一个法向量为
的一个法向量为 ,观察知二面角
,观察知二面角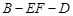 的平面角为锐角,所以其余弦值为
的平面角为锐角,所以其余弦值为 .
.
练习册系列答案
相关题目
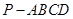 中,
中,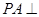 平面
平面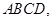 四边形
四边形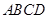 为正方形,
为正方形,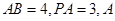 点在
点在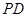 上的射影为
上的射影为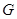 点.
点.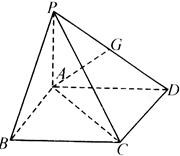
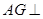 平面
平面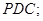
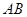 上是否存在一点
上是否存在一点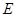 ,使得
,使得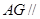 平面
平面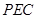 .若存在,求出
.若存在,求出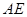 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD AE,BD
AE,BD
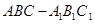 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则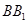 与平面
与平面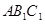 所成的角的大小为
所成的角的大小为 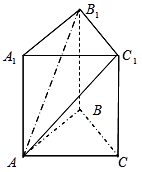
 表示平面,则以下命题正确的有( )
表示平面,则以下命题正确的有( ) ; ②
; ② ; ③
; ③ ; ④
; ④ .
. 为不重合的平面,
为不重合的平面, 为不重合的直线,则下列命题正确的是( )
为不重合的直线,则下列命题正确的是( ) ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,
, ,
, ,则
,则 ,则这个长方体的对角线长为__________
,则这个长方体的对角线长为__________