题目内容
4.已知函数f(x)=-$\frac{1}{3}$x3+2mx2+n(m,n,x∈R)图象上任意两点A(x1.y1),B(x2,y2)(x1>x2),满足f(x1)-f(x2)<3x1-3x2+x12-x22,则实数m的取值范围是[$\frac{1-\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$].分析 由题意得$\frac{1}{3}$x23-2mx22+3x2+x22<$\frac{1}{3}$x13-2mx12+3x1+x12,从而转化为证明g(x)=$\frac{1}{3}$x3-(2m-1)x2+3x在R上是增函数,求导解出即可.
解答 解:由题意得,
f(x1)=-$\frac{1}{3}$x13+2mx12+n,f(x2)=-$\frac{1}{3}$x23+2mx22+n,
则(-$\frac{1}{3}$x13+2mx12+n)-(-$\frac{1}{3}$x23+2mx22+n)<3x1-3x2+x12-+x22,
则$\frac{1}{3}$x23-2mx22+3x2+x22<$\frac{1}{3}$x13-2mx12+3x1+x12,
即$\frac{1}{3}$x23-(2m-1)x22+3x2<$\frac{1}{3}$x13-(2m-1)x12+3x1,
故g(x)=$\frac{1}{3}$x3-(2m-1)x2+3x在R上是增函数,
g′(x)=x2-2(2m-1)x+3,
故△=4(2m-1)2-4×1×3≤0,
解得,$\frac{1-\sqrt{3}}{2}$≤m≤$\frac{1+\sqrt{3}}{2}$.
故答案为:[$\frac{1-\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$].
点评 本题考查了函数的单调性的应用及导数的综合应用.

练习册系列答案
相关题目
14.设m>n,函数y=(x-m)2(n-x)的图象可能是( )
| A. | 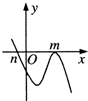 | B. | 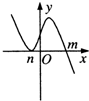 | C. | 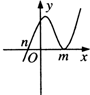 | D. | 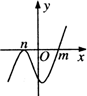 |
12.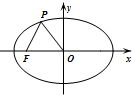 如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
 如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{30}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1 |
9.已知函数f(x)=$\frac{1}{{3}^{x}+2}$,则函数在(0,+∞)上( )
| A. | 单调递减且无最小值 | B. | 单调递减且有最小值 | ||
| C. | 单调递增且无最大值 | D. | 单调递增且有最大值 |