题目内容
10.计算1×2+2×3+…+n(n+1)的值为$\frac{1}{3}({n}^{3}+3{n}^{2}+2n)$.分析 由n(n+1)=n2+n,然后利用数列的分组求和得答案.
解答 解:∵n(n+1)=n2+n,
∴1×2+2×3+…+n(n+1)=(12+1)+(22+2)+(32+3)+…+(n2+n)
=(12+22+32+…+n2)+(1+2+3+…+n)
=$\frac{1}{6}n(n+1)(2n+1)+\frac{1}{2}n(n+1)$
=$\frac{1}{3}({n}^{3}+3{n}^{2}+2n)$.
故答案为:$\frac{1}{3}({n}^{3}+3{n}^{2}+2n)$.
点评 本题考查数列的分组求和,考查等差数列的前n项和,属中档题.

练习册系列答案
相关题目
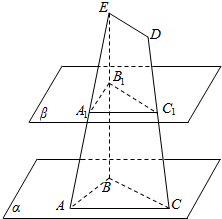 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积. 如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.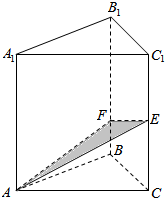 在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.
在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.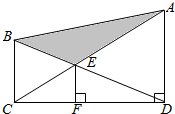 如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.
如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.