题目内容
1.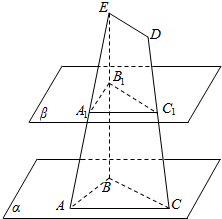 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
分析 由梯形中位线定理先求出B1C1,再由平面平行的性质求出A1B1和A1C1,然后利用余弦定理和正弦定理能求出△A1B1C1的面积.
解答 解:∵平面β∥α,∴A1B1∥AB,B1C1∥BC,
∵∠A1B1C1与∠ABC同向,
∴∠A1B1C1=∠ABC,
∵cos$∠ABC=\frac{{5}^{2}+{8}^{2}-{7}^{2}}{2×5×8}$=$\frac{1}{2}$,
∴∠A1B1C1=∠ABC=60°,
∵B1为EB的中位线,∴B1A1是△EAB的中位线,
∴A1B1=$\frac{1}{2}$AB=$\frac{5}{2}$,
同理,B1C1是梯形BCDE的中位线,
∴B1C1=$\frac{1}{2}(BC+DE)=5$,
∴sin∠A1B1C1=sin60°=$\frac{\sqrt{3}}{2}$,
∴△A1B1C1的面积:
S=$\frac{1}{2}×{A}_{1}{B}_{1}×{B}_{1}{C}_{1}×sin∠{A}_{1}{B}_{1}{C}_{1}$=$\frac{1}{2}$×$\frac{5}{2}×5×\frac{\sqrt{3}}{2}$=$\frac{25\sqrt{3}}{8}$.
点评 本题考查三角形的面积的求法,是中档题,解题时要认真审题,注意平面平行的性质、余弦定理和正弦定理的灵活运用.

练习册系列答案
相关题目
12.某地区汽车限行规定如下:
某地区某行政单位有车牌尾号为6的汽车A和尾号为9的汽车B,在非限行日,A车日出车频率为p,B车日出车频率为q,周六、周日和限行日停止用车,现将汽车日出车频率视为日出车概率,且A,B两车是否出车相互独立.
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
16.函数f(x)=log${\;}_{\frac{1}{4}}$(x2-9)的单调增区间是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (3,+∞) | D. | (-∞,-3) |
11.已知等比数列{an}的公比为q,Sn是{an}的前n项和,且满足:an+1=a1Sn+1(n∈N*),则下列结论正确的是( )
| A. | a1=2 | B. | a12<2015 | C. | q=2 | D. | S10>2015 |