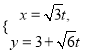题目内容
【题目】已知![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)增区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出![]() ,令
,令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)不等式
的减区间;(Ⅱ)不等式![]() 恒成立,等价于当
恒成立,等价于当![]() 时,
时, 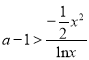 恒成立,只需
恒成立,只需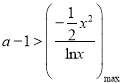 ,利用导数研究函数的单调性,求出
,利用导数研究函数的单调性,求出![]() 的最大值为
的最大值为![]() ,所以
,所以![]() ,
, ![]() .
.
试题解析:(Ⅰ) 依题意![]() ,
,
若![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,又
,又![]() ,
,
解得![]() ,所以函数
,所以函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(Ⅱ)依题意得![]() 即
即![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴ ![]() ,∴
,∴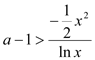 ,
,
∴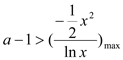 .
.
设![]()
![]() ,
, 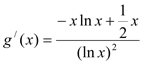 ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减;
单调递减;
∴![]() =
=![]() ,
,
∴![]() 即
即![]() .
.
【方法点晴】本题主要考查利用导数研究函数的单调性及求函数的最值、不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立
恒成立![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题(2)是利用方法 ① 求得
恒成立;④ 讨论参数.本题(2)是利用方法 ① 求得![]() 的取值范围.
的取值范围.

练习册系列答案
相关题目