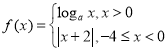题目内容
【题目】设命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ,命题
,命题![]() :实数
:实数![]() 满足
满足![]() .
.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)当![]() 时,求得不等式
时,求得不等式![]() 的解集.求得不等式组
的解集.求得不等式组![]() 的解集,根据
的解集,根据![]() 为真,得到
为真,得到![]() 均为真命题,对两个不等式的解集求交集,求得实数
均为真命题,对两个不等式的解集求交集,求得实数![]() 的取值范围.(2)由(1)得到不等式组
的取值范围.(2)由(1)得到不等式组![]() 的解集,求得不等式
的解集,求得不等式![]() 的解集,将“
的解集,将“![]() 是
是![]() 的充分不必要条件”转化为“
的充分不必要条件”转化为“![]() 是
是![]() 的充分不必要条件”,根据充分不必要条件的知识列不等式组,解不等式组求得
的充分不必要条件”,根据充分不必要条件的知识列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
解:(1)由![]() 得
得![]()
又![]() ,所以
,所以![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() ,
,
即命题![]() 为真命题时,实数
为真命题时,实数![]() 的范围是
的范围是![]()
由![]() 解得
解得![]() ,
,
即命题![]() 为真,则实数
为真,则实数![]() 的范围为
的范围为![]()
又![]() 为真,所以所求范围为
为真,所以所求范围为![]()
(2)若![]() 是
是![]() 的充分不必要条件
的充分不必要条件![]()
![]() 是
是![]() 的充分不必要条件
的充分不必要条件
设![]() ,
,![]() ,则
,则![]()
∴实数![]() 满足
满足 ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目