题目内容
若函数f(x)=
,其中[x]表示不大于x的最大整数,如[1.2]=1,则f(4.8)=( )
|
| A、8 | B、4 | C、2 | D、1 |
考点:函数的值
专题:函数的性质及应用
分析:由已知条件得f(4.8)=f([x])=f(4)=4
=2.
| 1 |
| 2 |
解答:
解:∵f(x)=
,其中[x]表示不大于x的最大整数,
∴[1.2]=1,
∴f(4.8)=f([x])=f(4)=4
=2.
故选:C.
|
∴[1.2]=1,
∴f(4.8)=f([x])=f(4)=4
| 1 |
| 2 |
故选:C.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
等差数列{an}的公差为2,a2+a8=16,则a6=( )
| A、6 | B、8 | C、10 | D、12 |
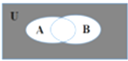 已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )
已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )| A、{3} |
| B、{4,5,6,7,8} |
| C、{7,8} |
| D、{1,2,7,8} |
函数y=cos(1+x2)+4的导数是( )
| A、2xsin(1+x2) |
| B、-sin(1+x2) |
| C、2cos(1+x2) |
| D、-2xsin(1+x2) |